ترجمههای کامران بزرگزاد

داستان معمایی که برای بیش از سیصد و پنجاه
سال باهوشترین اذهان بشر را به خود مشغول کرده بود.
’فکر کنم اینجا باید سخنانم را تمام کنم‘
23 ماه ژوئن سال 1993، دانشگاه کمبریج
تعدادِ بینهایت سهگانههای فیثاغورثی
از قضیه فیثاغورث تا آخرین قضیه فرما
دوران جداول،
چیستانها، و معماها
این کتاب
داستان آخرین قضیه فِرما را روایت میکند و روند تاریخی آن را از قرن ششم قبل از میلاد
تا اواخر قرن بیستم دنبال میکند. ریشه آخرین قضیه فرما به زمان فیثاغورث باز میگردد.
فصل اول کتاب
نیز به توضیح روند تاریخی این قضیه از دوران فیثاغورث میپردازد و بعد از مرور چند
بخش تاریخی کوتاه، به خود فِرما میرسد. داستان زندگی فرما و آخرین قضیه او با
تفصیل بیشتری در فصل دوم مطرح میشوند. در فصل سوم اولین تلاشهای ناموفقی که برای حل این
معما انجام گرفت مورد بررسی قرار میگیرند. از فصل چهارم به بعد نیز رویکردهای جدیدی
که در قرنهای نوزدهم و بیستم در رابطه با این قضیه اتخاذ شد، و نهایتاً به اثبات
آن توسط اندرو وایلز انجامید، مورد بررسی قرار میگیرند.
سطح این
کتاب مقدماتی است و مطالعه آن جز اندکی ریاضیات دبیرستانی هیچ پیشنیاز دیگری
ندارد. حتی اگر خواننده کتاب از حوزههای دیگری مثل علوم انسانی نیز آمده باشد، و
مطالب فنی مطرح شده را بطور کامل درک نکند، در عوض مطالب تاریخی مطرح شده در آن
فراوان است. نویسنده در این کتاب قصد ندارد جزئیات اثبات قضیه فرما را به خواننده
ارائه دهد، زیرا چنین چیزی بسیار فنی و پیشرفته است و به راحتی میتواند موضوع
چندین تِز دکترا باشد. همانطور که در این کتاب مطرح خواهد شد، این اثبات حاصل تلاش
مستمر یک ریاضیدان بااستعداد است، که تقریباً بیشتر عمر حرفهای خودش را صرف حل
مسئلهای کرده که بیش از سیصد و پنجاه سال لاینحل مانده بود. از این گذشته، کارهای
وایلز بر اساس کارهای دیگری است که بیشتر آنها حاصل ریاضیاتِ قرن بیستم است،
موضوعاتی که از لحاظ پیشرفته بودن دست کمی از اثبات اصلی وایلز ندارند (چیزهایی
مثل معادلات بیضوی، فرمهای ماجولار، حدس تانیاما-شیمورا، منحنی فرآی، نظریه ییواساوا،
روش کولیواگین-فلاک ...). پس نباید انتظار داشت بتوان جزئیات این اثبات را
در کتابی با این سطح، یا حتی کتابهایی که در سطح کارشناسی، یا کارشناسی ارشد ریاضی
نوشته میشوند، توضیح داد. آنچه در این کتاب بر آن تاکید میشود مفهوم اثبات
ریاضی، و اینکه این اثبات چقدر میتواند پیچیده باشد، است. البته این توضیحات
نباید موجب دلسردی خوانندگان جوان شود. هدف اصلی این کتاب تشریح روشهای
ریاضی، و تشویق دانشآموزان و دانشجویان به مطالعه این رشته است.
ممکن است
بسیاری از خوانندگان کتاب با آخرین قضیه فرما آشنایی داشته باشند. این قضیه بصورت
زیر است:
معادله
xn + yn = zn
برای nهایی که بزرگتر از 2 باشد، هیچ جواب صحیحی ندارد.
خوانندگانی
که اطلاع دقیقی از این معادله ندارند باید توجه کنند که وقتی گفته میشود معادله
فوق هیچ جوابی ندارد، منظور این است که ’هیچ جوابی ندارد که در آن x، y، و z اعداد صحیح باشند (1, 2, 3, …)‘، و الا معادله فوق
میتواند بینهایت جواب غیر صحیح داشته باشد که بصورت اعداد کسری و اعشاری هستند.
چیزی که کار را مشکل میکند، شرط داشتن جوابهای صحیح است. ظاهر این مسئله بقدری
ساده است که هر دانش آموز کلاس ششم ابتدایی نیز میتواند آن را درک کند. ولی
برخلاف ظاهر ساده آن، اثباتش چنان پیچیده است، که علیرغم همه تلاشهایی که
بهترین ریاضیدانان جهان برای حل آن کردند، برای مدتی بیش از سه قرن لاینحل مانده
بود.
این قضیه
برای اولین بار توسط پییر دو فرما مطرح شد. بعد از مدتی او ادعا کرد که اثباتی را
برای آن دارد، ولی بگفته خودش ”چون این اثبات طولانی است نمیتواند آن را در حاشیه
کتابش بنویسد“. پس از آنهم، فرما هیچ وقت اثبات خودش را در هیچ جای دیگری ارائه
نکرد (مانند بقیه کارهایش)، و علیرغم تلاشهای فراوانِ ریاضیدانان برای کشف
دوباره این اثبات، موضوع همچنان لاینحل ماند.
نهایتاً
چیزی که در اواخر قرن بیستم توسط اندرو وایلز بعنوان اثبات این قضیه مطرح شد،
آنچنان با ظاهر اولیه آن تفاوت داشت، که غیر ممکن است فرما چنین چیزی را بعنوان
اثبات خودش در نظر گرفته باشد. بر سر اینکه فرما حقیقتاً اثباتی برای این قضیه داشته
یا نه مناقشه وجود دارد. اعتقاد عمومی بر این است که فرما انسان شریفی بوده و دروغ
نمیگفته، ولی اگر آن چیزی که او در ذهنش بعنوان اثبات این قضیه پرورش داده بود
توسط دیگران مورد موشکافی قرار میگرفت، نهایتاً چیز اشتباهی در آن کشف میشد. عده
کمی هم بر این باورند که فرما حقیقتاً اثبات سادهای برای این مسئله پیدا کرده،
چیزی که تا کنون به ذهن هیچ کس نرسیده، و برخی هم در تلاش هستند تا آن اثبات گمشده
را پیدا کنند.
این کتاب
برای اولین بار در سال 1997، یعنی حدود 20 سال پیش منتشر شد. ولی بنا به دو دلیل
اصلاً از ارزش آن کاسته نشده. اول اینکه این کتاب یک کتابِ خوبِ عمدتاً تاریخی است
و کُتب (خوب) تاریخی به آسانی منسوخ نمیشود. و دلیل دوم، و مهمتر، این است که این
کتاب چیزی را شرح میدهد که برای بیش از سه قرن بزرگترین مغزهای بشر درگیر آن بودهاند.
چگونه چنین چیزی میتواند ظرف مدت بیست یا پنجاه یا ... سال منسوخ شده و به موضوع
پیش و پا افتادهای بدل شود؟ من حدود 8 سال پیش با این کتاب آشنا شدم، و از همان
موقع قصد داشتم آن را ترجمه کنم، ولی متاسفانه فرصت آن حاصل نشد. این کتاب یکی از
بهترین کتابهایی است که در سطح مقدماتی درباره آخرین قضیه فرما نگاشته شده و در
زمان خودش مقبولیت بینالمللی فراوانی پیدا کرد، و تا مدتها جزء پرفروشترین
کتابهای عامه فهم علمی بود. بهمین دلیل جای آن بود که خیلی وقت پیش به فارسی ترجمه
میشد و در اختیار علاقمندان قرار میگرفت.
تفاوتی که
کتاب حاضر با نسخه اصلی دارد اضافه شدن تصاویر به آن است، که اینکار توسط مترجم
انجام گرفته و از این لحاظ نسخه فارسی کاملتر از نسخه اصلی کتاب است.
سایمون
سینگ (SIMON SINGH)، نویسنده هندی تبار این کتاب
در سال 1964 در سامرست انگلستان بدنیا آمد. تحصیلات او در زمینه فیزیک بود، و در
سال 1996 مدرک دکترای خودش را در رشته فیزیک ذرات بنیادی از کالج امانوئل
در کمبریج اخذ کرد. او بیشتر از اینکه بعنوان یک فیزیکدان شناخته شود، بیشتر
بعنوان یک مستندساز تلویزیونی شناخته میشود. او در ساختن بسیاری از مستندات برای
شبکههای مختلف مشارکت داشته. کتاب حاضر از یک مستند تلویزیونی اقتباس شده که سینگ
آن را در سال 1996 برای برنامه Horizon
بیبیسی ساخت. کلیه مصاحبههایی که در این کتاب به آنها اشاره میشود، مشروح همان
مصاحبههایی هستند که در این مستند تلویزیونی نشان داده میشوند، ولی نسبت به آنها
خیلی مفصلترند. در تکمیل مطالعه این کتاب، خوانندگان علاقهمند میتوانند به این
مستند تلویزیونی نیز رجوع کنند. این فیلم یک ساعته بر روی اینترنت موجود است و با
جستجوی مختصری میتوان آن را پیدا کرد. برای یافتن آن فقط کافیست کلمات کلیدی ”Fermat's Last Theorem TV
Simon Singh “ را جستجو کنید.
در اینجا
لازم میدانم از ریاضیدان فقید ایرانی، پرفسور مریم میرزاخانی یاد کنم که خیلی زود
از میان ما رفت. حدود ده/دوازده سال پیش بود که با نام او آشنا شدم و از همان موقع
تحت تاثیر موفقیتهای او قرار گرفتم. ممکن است بدانید که بزرگترین جایزه مطرح در
ریاضیات، چیزی بنام مدال فیلدز است، و مریم میرزاخانی با خدماتی که به
دنیای ریاضیات کرده بود توانست آن جایزه را کسب کند، جایزهای که حتی کسی مثل
اندرو وایلز هم موفق به گرفتن آن نشد. البته اینکه وایلز آن جایزه را دریافت نکرد
دلیل آشکاری دارد، و آن هم این است که این جایزه تنها میتواند نصیب کسانی شود که
زیر چهل سال سن دارند، و موقعی که اندرو وایلز کارهایش را برای جهان افشا کرد حدود
چهل و یک سال داشت. مطمئناً اگر سن او کمتر بود، برای دریافت این جایزه هیچ کس از
او سزاوارتر نبود. مدال فیلدز بزرگترین جایزه و افتخاری است که یک ریاضیدان میتواند
به آن دست یابد، چیزی که مریم میرزاخانی با کارهای درخشان خودش به آن دست یافته
بود. من نمیدانم که آیا او با وایلز بطور نزدیک آشنایی داشته یا نه، ولی مطمئن
هستم آنها با کارهای یکدیگر آشنا بودند. زمانی که وایلز اثبات خودش را برای آخرین
قضیه فرما ارائه داد، مریم تنها شانزده سال داشت (1372). ولی درست در همان سال او
اولین مدال طلای خودش را در المپیاد جهانی ریاضی کسب کرد. مطمئناً در آن زمان او
با آخرین قضیه فرما آشنایی داشت و از دشواریهای آن آگاه بود، و احتمالاً خبر
اثبات این قضیه توسط وایلز او را در یادگیری ریاضیات مصممتر کرده بود. در این
کتاب شما با موضوعاتی برخورد میکنید که زنان در طول تاریخ برای ورود به ریاضیات
با آن روبرو بودهاند. در روزگار ما ظاهراً خبری از چنین دشواریهایی نیست. در ظاهر
مانع زیادی برای زنان دیده نمیشود، ولی مانند همه چیز، حتی امروز نیز این علم تا
حد زیادی در تسلط مردان قرار دارد. وجود کسانی مانند مریم میرزاخانی استثناء است و
باید آن را به فال نیک گرفت و در جهت فراگیر شدن این علم میان دختران جوان تلاش
کرد. باید گفت که فعالیت ریاضی هیچ نیازی به جنسیت ندارد. نه قوای بدنی میخواهد و
نه فیزیولوژی خاص. تنها لازمه درخشش در آن داشتن یک ذهن پویا و کنجکاو است، که
بدون هیچ بهانهای هم در میان زنان وجود دارد و هم در میان مردان.
تابستان
امسال خبر فقدان او را شنیدیم. گذشته از اینکه در فرهنگ ما همیشه خبر جوانمرگ
شدنِ کسی غمانگیز است، ولی شخصیتی که او طی این سالها از خودش نشان داده بود مزید
بر این غم شد؛ یک مادر خوب، انسانی ساده و خوشخلق، ... و البته نابغه.
به امید
شکوفایی مریمهای بیشتر، ترجمه این کتاب را به او تقدیم میکنم.

مریم
میرزاخانی (1396-1356)
یادش تا
ابد گرامی باد.
زمستان 1396،
کامران بزرگزاد ایمانی
داستان آخرین
قضیه فِرما بطور ناگزیری به تاریخ ریاضیات پیوند خورده، بطوری که اکثر حوزههای
نظریه اعداد تحت تاثیر آن قرار گرفتهاند. این قضیه بینش بیهمتایی را فراهم آورد
که باعث پیشرفت ریاضیات شد و شاید مهمتر از همه، الهامبخش بسیاری از ریاضیدانان
بود. آخرین قضیه فرما اساس حماسههایی را تشکیل میدهد که شامل تلاشها، تقلبها،
دسیسهها و مصیبتهایی است که بزرگترین ریاضیدانان تاریخ با آن روبرو بودهاند.
ریشه
آخرین قضیه فرما در ریاضیات یونان باستان است، یعنی حدود دو هزار سال پیش از اینکه
پییر دو فرما (Pierre de Fermat)
مسئله را به شکلی که ما اکنون میشناسیم مطرح کند. بنابراین این قضیه موجب پیوند
میان ریاضیات پیچیده کنونی و اصول ریاضی کهن میشود که دو هزار سال پیش توسط
فیثاغورث ایجاد شد. ساختاری که من برای نگارش این کتاب انتخاب کردهام عمدتاً از
یک ترتیب تاریخی برخوردار است که با شرح رسوم انجمن فیثاغورثیان شروع میشود، و با
داستان تلاش اندرو وایلز برای حل معمای فرما پایان میپذیرد.
در فصل
اول کتاب من داستان فیثاغورث، و اینکه چرا قضیه فیثاغورث ریشه اصلی آخرین قضیه
فرما است، را شرح میدهم. همچنین این فصل شامل برخی مفاهیم اساسی ریاضیات است که
در سراسر کتاب مطرح میشوند. فصل دوم کتاب داستان را از یونان باستان تا فرانسه
قرن هفدهم، یعنی جایی که پییر دو فرما برجستهترین معمای تاریخ ریاضیات را مطرح
کرد، دنبال میکند. به منظور توصیف شخصیت برجسته فرما و سهمی که او در ریاضیات از
آن برخوردار بود (و این سهم فراتر از آخرین قضیه اوست) من چند صفحهای را به زندگی
و کارهای برجسته دیگر او اختصاص دادهام.
در فصلهای
3 و 4 تلاشهایی را شرح میدهم که در طول قرون هجدهم و نوزدهم برای اثبات آخرین
قضیه فرما صورت گرفت. هر چند این تلاشها نهایتاً به شکست انجامیدند، ولی آنها
ابزارها و تکنیکهای ریاضی قدرتمندی را فراهم آوردند که وجود برخی از آنها برای
اثبات نهایی این قضیه حیاتی هستند. علاوه بر توضیح ریاضیات مربوط به آخرین قضیه
فرما، من بیشتر این فصول را به ریاضیدانانی اختصاص دادهام که همیشه در طول تاریخ
با آخرین قضیه فرما درگیر بودهاند. قصه آنها نشان میدهد که چگونه ریاضیدانان
حاضرند برای بدست آوردن حقیقت همه چیز را فدا کنند، و چگونه در طول این قرون
ریاضیات تحول یافته است.
فصول آخر
کتاب تاریخچه رویدادهای مهمی است که در چهل سال اخیر روی داده و بررسی آخرین قضیه
فرما را متحول کرده است. به ویژه در فصول 6 و 7، ما بر روی کارهای وایلز تمرکز میکنیم،
که در اواخر قرن بیستم موجب حیرت ریاضیدانان گشت. این فصول بر پایه مصاحبههای
مفصلی قرار دارند که با وایلز صورت گرفت. این برای من فرصت بیهمتایی را فراهم
آورد تا بطور مستقیم شنونده یکی از خارقالعادهترین رویدادهای ریاضی قرن بیستم
باشم و امیدوارم توانسته باشم شجاعت و خلاقیت بینظیری را که وایلز در طول ده سال
از خودش نشان داد به شما منتقل کنم.
برای
اینکه قصه پییر دو فرما و معمای حیرتانگیز او را برای شما نقل کنم، مجبورم بدون
اینکه به معادلات متوسل شوم برخی مفاهیم ریاضی را برای شما شرح دهم، ولی گاهگاهی
سر و کله x، y و z در این کتاب ظاهر میشود،
و چنین چیزی اجتناب ناپذیر است. هنگامی که مجبور باشم در این کتاب معادلاتی را
مطرح کنم، تلاش خواهم کرد تا آنقدر در مورد آنها توضیح دهم که حتی خوانندگانی که
هیچ نوع زمینه ریاضی ندارند هم بتوانند اهمیت آنها را درک کنند. برای خوانندگانی
که تجربه بیشتری در موضوعات مربوطه دارند، من ضمیمههایی را فراهم آوردهام که
ایدههای ریاضی مطرح شده در متن اصلی را بسط میدهد. علاوه براین، فهرستی از کتابهایی
را آوردهام که عمدتاً به خوانندگان غیر فنی کمک میکنند تا درک عمیقتری از حوزههای
ریاضی مطرح شده بدست آورند.
نوشتن این
کتاب بدون یاری گرفتن از خیلیها ممکن نبود. به ویژه مایلم از اندرو وایلز تشکر
کنم، که در مدت زمان کوتاهی فرصت یک مصاحبه طولانی و مفصل را برای من فراهم آورد.
در طول هفت سالی که من روزنامهنگار علمی بودم، هیچ وقت کسی را ملاقات نکرده بودم
که تا این اندازه به کار خود اشتیاق و تعهد داشته باشد، و از این بابت تا ابد
قدردان پرفسور وایلز هستم که مرا در داستان خودش شریک کرد.
همچنین
مایلم از ریاضیدانان دیگری که اجازه دادند با آنها مصاحبههای طولانی داشته باشم و
مرا در نوشتن این کتاب یاری دادند تشکر کنم. برخی از آنها شاهد وقایع تاریخی چهل
سال اخیر بودهاند. ساعاتی که من با آنها مشغول گفتگو بودم بسیار مسرت بخش بود و
از صبر و اشتیاق آنها برای توصیف بسیاری از مفاهیمِ ریاضی زیبا تشکر میکنم. به
ویژه مایلم از جان کوتز (John Coates)،
جان کانوی (John Conway)، نیک کَتز (Nick Katz)، بَری مِیزر (Barry Mazur)، کن ریبِت (Ken Ribet)، پیتر سارناک (Peter Sarnak)، گورو شیمورا (Goro Shimura)، و ریچارد تیلور (Richard Taylor) تشکر کنم.
نهایتاً
باید بگویم که بسیاری از مصاحبههایی که در این کتاب صورت گرفته، فقط وقتی امکانپذیر
شدهاند که من مشغول ساختن یک مستند تلویزیونی درباره آخرین قضیه بودهام. در
اینجا مایلم از BBC بخاطر اینکه به من
اجازه دادند در کتاب خودم از این مطالب استفاده کنم تشکر کنم. همچنین به جان لینچ
بابت همکاری که در ساخت این مستند داشت مدیون هستم.
سایمون
سینگ،
1997
اگر
اسکلیس[1] فراموش شود، بااینحال همه ارشمیدس را بخاطر خواهند داشت، زیرا
گرچه زبانها میمیرند اما ایدههای ریاضی همیشه زنده میمانند. شاید ’جاودانگی‘
لغت پوچی باشد، اما معنی آن هرچه باشد، احتمال دارد یک ریاضیدان شانس این را داشته
باشد که از جاودانگی برخوردار شود.
ج.اچ. هاردی
این
مهمترین درس ریاضی قرن بود. دویست ریاضیدان در جای خود میخکوب شده بودند. تنها یک
چهارم آنها میتوانست از علائم یونانی و جبری که بطور فشرده بر روی تخته سیاه نوشته
شده بود بطور کامل سر در آورند. بقیه آنها تنها نظارهگر چیزی بودند که امیدوار
بودند یک رویداد تاریخی واقعی باشد.
از روز
قبل شایعاتی پخش شده بود. ایمیلهایی که برای ریاضیدانان فرستاده شده بود به این
اشاره میکرد که این درس به آخرین قضیه فرما، یعنی مشهورترین مسئله ریاضی، مربوط
است. چنین شایعاتی غیر معمول نبودند. معمولاً در گروه ریاضی دانشگاهها موضوع
آخرین قضیه فرما هنگام صرف چای به میان میآمد، و ریاضیدانان درباره اینکه چه کسی
مشغول چه کاری است با یکدیگر صحبت میکردند. گاهی اوقات صحبتهایی که ریاضیدانان با
یکدیگر داشتند گمانهزنیهای موجود را به شایعاتی بدل میکرد که شاید در اینمورد
پیشرفت غیر منتظرهای حاصل شده، ولی چنین چیزی تاکنون اتفاق نیافتاده بود.
اما
اینبار شایعات متفاوت بودند. یک دانشجوی محقق از این بابت آنقدر مطمئن بود که 10
پوند شرط بسته بود که آخرین قضیه فرما ظرف این هفته حل خواهد شد. ولی موسسه شرطبندی
از قبول شرط او سرباز زد. این پنجمین دانشجویی بود که در آن روز به آنها رجوع کرده
بود و میخواست دراینمورد شرطبندی کند. آخرین قضیه فرما برای بیش از سه قرن موجب
سردرگمی بسیاری از ریاضیدانان جهان شده بود، ولی حالا حتی شرطبندها نیز به این شک
داشتند که این مسئله همچنان لاینحل بماند.
سه تا از
تخته سیاهها با محاسبات مختلف پر شده بود و مدرس مکثی کرد. اولین تخته پاک شد و
عملیات جبری ادامه یافت. بنظر میرسید هر خطی که نوشته میشود قدمی بسوی حل مسئله
نزدیکتر میگردد، ولی با گذشت سی دقیقه هنوز مدرس اثبات قضیه را اعلام نکرده بود.
اساتیدی که در جلو نشسته بودند بیصبرانه منتظر اعلام نتیجه بودند. دانشجویانی که
در عقب ایستاده بودند به ارشدهای خود نگاه میکردند تا شاید از آنها نشانهای مبنی
بر نتیجه دریافت کنند. آنها پیش خود فکر میکردند که آیا آنچه شاهد آن هستند اثبات
کامل قضیه فرما است، یا اینکه مدرس تنها قصد دارد یک استدلال ناقص را مطرح کند؟
مدرس این
درس اندرو وایلز (Andrew Wile)
بود، یک ریاضیدان انگلیسی کم حرف که از دهه 1980 به آمریکا مهاجرت کرده بود و سمتِ
استادی دانشگاه پرینستون را داشت، جایی که او بعنوان یکی از بااستعدادترین
ریاضیدانان عصر خودش مطرح شده بود. ولی در سالهای اخیر او تقریباً از کنفرانسها و
سمینارهای سالانه کناره گرفته بود، و همکارانش تصور میکردند که دوران شکوفایی
وایلز به پایان رسیده. این غیر معمول نیست که کار یک ریاضیدان به یکباره تمام شود،
نکتهای که ریاضیدانی بنام آلفرد آدلر به آن اینطور اشاره میکند: ”زندگی
ریاضی یک ریاضیدان کوتاه است. بعد از سنین بیست و پنج یا سی سالگی، کارهای آنها
بندرت پیشرفت میکند، و اگر هم بعد از این سنین چیزی حاصل شود، بازده زیادی نخواهد
داشت.“
جی.اچ
هاردی (G.H.Hardy) در کتاب اعترافات یک
ریاضیدان میگوید: ”ریاضیدانانِ جوان باید مشغول اثبات قضایا، و ریاضیدانان
پیر باید مشغول نوشتن کتاب شوند. هیچ ریاضیدانی نباید فراموش کند که ریاضیات بیش
از هر هنر یا علم دیگری، یک بازی مختص جوانان است. برای اینکه این را بهتر نشان
دهم، به این نکته اشاره میکنم که متوسط سن عضویت در جامعه سلطنتی علوم برای
ریاضیدانان نسبت به بقیه از همه کمتر است.“ بااستعدادترین دانشجوی هاردی، یعنی سرینیواسا
رامانوجان (Srinivasa Ramanujan)،
تنها سی و یک سال داشت که به عضویت جامعه سلطنتی درآمد، و در سنین جوانی توانست یک
سری پیشرفتهای مهم را حاصل کند. برخلاف اینکه رامانوجان در دهکده موطن خودش
کامباکونام در جنوب هند، تحصیلات اندکی را حاصل کرد، او توانست قضایا و راه حلهایی
را پیدا کند که از چشم ریاضیدانان غربی پنهان مانده بودند. ظاهراً در ریاضیات
تجربهای که با افزایش سن حاصل میشود، نسبت به درک و جسارتی که در جوانی
وجود دارد از اهمیت کمتری برخوردار است. هنگامی که رامانوجان نتایج کارهای خودش را
برای هاردی به کمبریج فرستاد، او چنان تحت تاثیر کارهای رامانوجان قرار گرفت که از
او خواست کار خودش را بعنوان یک حسابدار خوردهپا در جنوب هند رها کند و به
ترینیتی کالج لندن بیاید، جایی که او میتوانست با برجستهترین متخصصین نظریه
اعداد تعامل داشته باشد. متاسفانه زمستانهای سرد شرق انگلستان با مزاج رامانوجان
که به مناطق گرمسیری عادت داشت سازگار نبود، و او پس از ابتلا به مرض سل در سن 33
سالگی درگذشت.
ریاضیدانان
دیگری نیز بودند که از چنین استعدادی برخوردار بودند ولی دوران کاری آنها کوتاه
بود. ریاضیدان نروژی قرن نوزدهم، نیلز هنریک آبل (Niels Henrik Abel)، تنها نوزده سال داشت که بزرگترین
سهم خود به ریاضیات را ادا کرد، و هشت سال بعد، او نیز بواسطه ابتلا به سل در
تنگدستی کامل جان سپرد. چارلز هرمیت (Charles
Hermite) درباره آبل اینطور میگوید: ”او در ریاضیات چنان
میراثی از خودش باقی گذاشت که ریاضیدانان را برای پانصد سال مشغول نگاه میدارد“،
و این حرف کاملاً درستی است. اکتشافات آبل امروزه در کارهای متخصصین اعداد نقش
عمدهای دارد. اواریست گالوا (Evariste
Galois)، که یکی از معاصران آبل بود و به همان اندازه
بااستعداد بود، درحالی که هنوز 18 یا 19 سال سن داشت اکتشافات مهم ریاضی خود را
انجام داد، و در سن 21 سالگی درگذشت.
من این
نمونهها را از این جهت مطرح نکردم تا بگویم ریاضیدانان بااستعداد همیشه بطور
مصیبتباری جوانمرگ میشوند، بلکه میخواهم به این نکته اشاره کنم که مهمترین ایدههای
ریاضی بیشتر اوقات در سنین جوانی حاصل میشوند، و هاردی یکبار دراینمورد گفت ”من
هیچ اکتشاف عمده ریاضی را نمیشناسم که بعد از سنین پنجاه سالگی یک ریاضیدان حاصل
شده باشد.“ ریاضیدانان میانسال غالباً به پشت صحنه میروند و بجای تحقیق، سالهای
باقیمانده عمر خود را یا به تدریس و یا پستهای مدیریتی سپری میکنند. اندرو وایلز
هم از این قاعده مستثنی نبود. هرچند او حالا به سن چهل سالگی رسیده بود، ولی هفت
سال اخیر را در اختفای کامل کار میکرد، و تلاش او بر این بود که مهمترین مسئله
ریاضیات را حل کند. در حالی که خیلیها تصور میکردند کار وایلز تمام است، او
پیشرفتهای مهمی را بدست آورده بود و تکنیکها و ابزارهای جدیدی را اختراع کرده
بود و حالا میخواست آنها را آشکار کند. تصمیم او برای کار در انزوا خطر بالایی را
در برداشت، و مهمتر از همه، امکان داشت در دنیای ریاضیات گمنام شود.
در نبود
حق اختراع، گروههای ریاضی دانشگاهها جای مناسبی برای مخفی نگاه داشتن ایدهها
نیستند. اینکه ریاضیدانان میتوانند ایدههای خود را در زمان صرف چای و بیسکویت با
یکدیگر به اشتراک بگذارند مایه مباهات آنها است. به همین دلیل هم هست که
بسیاری از مقالات ریاضی چاپ شده توسط تیمی از ریاضیدانان نوشته میشوند که با هم
همکارند، و در نتیجه افتخار آنهم بطور مساوی میان آنها تقسیم میشود. ولی اگر
حقیقتاً پرفسور وایلز خودش به تنهایی میتوانست اثبات کاملی برای آخرین قضیه فرما
پیدا کند، آنگاه مهمترین جایزه ریاضی جهان نیز تنها نصیب خود او میشد. ولی بهایی
که او میبایست برای این پنهانکاری پرداخت کند این بود که نباید هیچ یک از ایدههایش
را با جامعه ریاضیدانان درمیان بگذارد یا آنها را مورد آزمون آنها قرار دهد، و
بنابراین احتمال زیادی بود که او مرتکب اشتباهات اساسی شود.
بطور
مطلوب وایلز میخواست زمان بیشتری را صرف مقاله خودش کند تا بتواند آن را بطور
کامل بررسی کند. ولی در آن زمان یک فرصت نادر پیش آمد تا او بتواند کشف خودش را در
موسسه آیزاک نیوتون در کمبریج مطرح کند و بخاطر همین احتیاط را کنار گذاشت.
هدف اصلی این موسسه این بود که بااستعدادترین مغزهای جهان را برای چند هفته دور هم
جمع کند تا درباره آخرین پیشرفتهای حاصله در تحقیقاتشان سمینارهایی را ارائه دهند.
ساختمان این موسسه که در حومههای دانشگاه کمبریج قرار داشت، به دور از تجمع
دانشجویان و چیزهای دیگری که میتوانست موجب هواسپرتی شود ساخته شده بود، طوری که
دانشگاهیان میتوانستند بر روی همکاریهای مشترک متمرکز شوند. هیچ راهرو بنبستی
در آنجا نبود که بتوان در آن مخفی شد و هر دفتری روبروی یک مجمع قرار داشت. قرار
بود که ریاضیدانان وقت خود را در این محوطه باز بگذرانند و به آنها توصیه میشد تا
درهای دفاتر خود را نبندند. حتی وقتی آنها در رفت و آمد بودند، بازهم تشویق میشدند
که این همکاری را ادامه دهند. حتی در آسانسور یک ساختمان سه طبقه نیز یک تخته سیاه
قرار داشت. در واقع تمام اطاقهای ساختمان حداقل دارای یک تخته سیاه بودند، از
جمله دستشوییها. در این زمان سمینارهایی که در موسسه نیوتون برگذار میشد درباره
’توابع-L و حساب‘ بودند. بزرگترین
متخصصین نظریه اعداد در اینجا جمع شده بودند تا مسائلی که به این حوزه کاملاً
تخصصی ریاضیات اختصاص داشت را باهم درمیان بگذارند، ولی این تنها وایلز بود که میدانست
کلید حل آخرین قضیه فرما توابع-L (L-functions) هستند.
هر چند
همه مایل بودند تا فرصت این را داشته باشند تا کشفیات خودشان را در مقابل چنین
مخاطبین برجستهای مطرح کنند، ولی دلیل اصلی که وایلز میخواست اینکار را در موسسه
نیوتون انجام دهد این بود که کمبریج شهر او بود. کمبریج جایی بود که در آنجا بدنیا
آمده و بزرگ شده بود. اینجا همان جایی بود که اولین نشانههای علاقه به اعداد در
او ظهور کرده بود، و همین جا بود که برای اولین بار با مسئلهای روبرو شد که بقیه
عمرش را به آن مشغول بود.
در سال
1963، هنگامی اندرو وایلز ده سال داشت، از قبل مجذوب ریاضیات شده بود. او میگوید:
”من همیشه عاشق این بودم که مسائل را در مدرسه حل کنم، بعضی وقتها هم آنها را به
خانه میبردم و خودم از روی آنها مسائل جدیدی میساختم. ولی بهترین مسئلهای که
پیدا کردم، در کتابخانه عمومی بود.“
یک روز
وقتی وایلز جوان از مدرسه به خانه بازمیگشت تصمیم گرفت سری به کتابخانه عمومی
میلتون رود بزند. این کتابخانه در مقایسه با کتابخانههای دانشگاهی محقر بود، ولی
چیزی که فراوان داشت یک مجموعه غنی از کتابهای معما بود، و همین توجه وایلز را به
خودش جلب کرد. این کتابها از همه گونه معماهای علمی و ریاضی پر بودند، و معمولاً
جواب این مسائل در صفحات آخر کتاب آمده بود. ولی اینبار کتابی که وایلز با آن
روبرو شده بود تنها حاوی یک مسئله بود و در انتهای کتاب هم هیچ جوابی برای آن
نیامده بود. نام این کتاب ’آخرین مسئله‘، نوشته اریک تمپل ِبل (Eric Temple Bell) بود. در این کتاب مسئلهای
مطرح میشد که ریشه در ریاضیات یونان باستان داشت، ولی فقط در قرن هفدهم به بلوغ
کامل رسیده بود. در آن موقع بود که یک ریاضیدان فرانسوی بنام پییر فِرما آن را
بعنوان چالشی برای بقیه ریاضیدانان جهان مطرح کرد. به مدت بیش از سه قرن
ریاضیدانان یکی پس از دیگری درمقابل میراث فرما مغلوب شده بودند و هیچ کس نتوانسته
بود آن را حل کند. مسائل حل نشده دیگری نیز در ریاضیات هستند، ولی چیزی که مسئله
فرما را از بقیه متمایز میکند سادگی فریبنده آن است. سی سال پس از خواندن کتاب
بِل، وایلز به من گفت که وقتی در آن لحظه با آخرین قضیه فرما آشنا شد چه احساسی
داشت: ’این مسئله خیلی ساده بنظر میرسید، ولی بااینحال همه ریاضیدانان بزرگ تاریخ
نتوانسته بودند آن را حل کنند. این مسئلهای بود که من، یعنی یک پسر بچه ده ساله،
میتوانست آن را درک کند، و آن موقع بود که فهمیدم هرگز اجازه نمیدهم این مسئله از
یادم برود. من باید آن را حل کنم.‘
مسئله
خیلی ساده بنظر میرسید زیرا بر پایه یک قضیه کوتاه ریاضی قرار داشت که هر کسی میتوانست
آن را بخاطر بسپارد، و آن هم چیزی نبود جز قضیه فیثاغورث:
در یک مثلث-قائمالزاویه،
مربع وتر با مجموع مربعات دو ضلع دیگر برابر است.
اگر
نگوییم این شعر کوتاه فیثاغورثی در مغز میلیاردها انسان حک شده، باید گفت میلیونها
نفر آن را از دوران مدرسه بیاد دارند. این یک قضیه ساده ریاضی است که هر کودک
دبستانی باید آن را یاد بگیرد. هر چند یک بچه ده ساله هم میتواند قضیه فیثاغورث
را درک کند، ولی همین قضیه ساده موجب الهام برای مسئلهای شد که بزرگترین
ریاضیدانان تاریخ را قرنها به خودش مشغول کرد.
فیثاغورث (Pythagoras)
که از اهالی ساموس (Samos) بود، یکی از
تاثیرگذارترین چهرهها در تاریخ ریاضیات است. بدلیل اینکه هیچ اطلاع دست اولی از
زندگی و کارهای او در دست نیست، آنچه از زندگی او نقل شده آمیختهای از حماسه و
افسانه است، و به همین دلیل برای تاریخنگاران مشکل بود تا حقایق را از افسانهها
جدا کنند. آنچه درباره فیثاغورث محقق است این است که او ایده منطقِ عددی را توسعه
داد و سهم عظیمی در اولین دوران طلائی ریاضیات داشت. به واسطه نبوغ او، از اعداد
فقط برای شمارش و محاسبه استفاده نمیشد، بلکه آنها جایگاه خودشان را داشتند. او
ویژگیهای اعداد خاص، و رابطه میان آنها و الگوهایی که از آن برخوردار بودند را
بررسی کرد. او فهمید که وجود اعداد مستقل از جهان محسوس ما است، و بنابراین مطالعه
آنها ربطی به کمدقتی ادراک ما ندارد. این یعنی او میتوانست حقایقی را کشف کند که
مستقل از نظرات یا پیشداوریها بودند و نسبت به دانشهای قبلی قطعیتر بودند.
فیثاغورث
که در قرن ششم قبل از میلاد زندگی میکرد، مهارتهای ریاضی خود را از راه سفرهایی
که در جهان باستان انجام میداد حاصل کرد. در بعضی داستانها، گستره سفرهای او را
به هند و بریتانیا نیز میرسد، ولی چیزی که بیشتر محقق است این است که او بسیاری
از تکنیکها و ابزارهای ریاضی را از اهالی مصر و بابل آموخت. در این دو قوم
باستانی سطح ریاضیات از محدوده شمارش ساده فراتر رفته بود، طوری که آنها میتوانستند
محاسبات پیچیدهای را انجام دهند که آنها را قادر میکرد سیستمهای مالی پیچیدهای
را ایجاد، و ساختمانهای دقیقی را بنا کنند. آنها حقیقتاً ریاضیات را فقط ابزاری
برای حل مسائل عملی میدیدند؛ انگیزهای که موجب کشف برخی قواعد هندسه شد این بود
که به آنها اجازه میداد محدوده زمینهایی که پس از طوفان سالانه رود نیل از بین
میرفتند را دوباره بازسازی کنند. خود لغت هندسه به معنای ’ اندازهگیری زمین‘
است.
فیثاغورث
میدید که مصریان و بابلیان محاسبات خودشان را با پیروی از یک سری دستورالعملها
انجام میدادند، دستورالعملهایی که میتوانست کورکورانه انجام شود. این
دستورالعملها، که نسل به نسل منتقل شده بودند، همیشه جواب درست میدادند و هیچ کس
بخودش زحمت نمیداد درستی آنها، یا منطق زیربنایی آنها را مورد پرسش قرار دهد.
چیزی که برای این تمدنها مهم بود این بود که این محاسبات درست عمل میکردند-
اینکه چرا درست عمل میکردند اهمیتی نداشت.
پس از
بیست سال سفر، فیثاغورث کلیه قواعد ریاضی جهان خودش را فرا گرفته بود. پس از آن
بسوی وطن خودش، جزیره ساموس واقع در دریای اژه، عزیمت کرد تا در آنجا مدرسهای را
تاسیس کند که به مطالعه فلسفه، و بویژه یافتههای ریاضی جدید او اختصاص داشت. او
نمیخواست صرفاً از اعداد استفاده کند، بلکه میخواست آنها را درک کند. او امیدوار
بود شاگردانی را پیدا کند که فکر بازی داشتند و بتوانند در توسعه ایدههای جدید به
او کمک کنند. ولی در طول غیاب او، فردی یاغی بنام پلیکراتس جزیره سوماس را که
زمانی آزادیخواه بود به یک جامعه متعصب و محافظهکار تبدیل کرده بود. پلیکراتس
از فیثاغورث دعوت کرد تا به دربار او بپیوندد، ولی فیلسوف ما متوجه شد که این تنها
نقشهای برای ساکت کردن او است و بنابراین دعوت پلیکراتس را رد کرد. در عوض او
شهر را ترک کرد و به غاری دور افتاده در جزیره پناه برد، جایی که میتوانست بدون
ترس از تعقیب به تفکر بپردازد.
انزوا به
مزاج فیثاغورث خوش نیامد و سرانجام تصمیم گرفت پسری را بعنوان اولین شاگرد خودش
قبول کند. هویت این پسر جوان معلوم نیست، ولی برخی مورخان بر این عقیدهاند که نام
او نیز فیثاغورث بوده و بعدها از این نظر معروف شده بود که اولین کسی بود که به
ورزشکاران توصیه کرده بود باید برای افزایش توان خود گوشت بخورند. فیثاغورثِ استاد
برای هر درس سه سکه به شاگرد خودش میداد. استاد متوجه شد که بیمیلی اولیه شاگردش
پس از سپری شدن چند هفته به اشتیاق فراوانی برای یادگیری دانش بدل شد. فیثاغورث
برای اینکه ببیند شاگردش واقعاً خواهان کسب دانش است وانمود کرد که در ازای هر
درسی که میدهد دیگر نمیتواند به او پولی پرداخت کند و این درسها باید متوقف
شوند. در آن موقع بود که خود شاگرد پیشنهاد کرد که هزینه تحصیلاتش را خودش پرداخت
کند. این شاگرد مرید فیثاغورث شد و تنها شاگرد او در ساموس بود. فیثاغورث در آنجا
مدرسهای را بطور موقت تاسیس کرد که ’نیمدایره فیثاغورث‘ نامیده میشد، ولی
نظرات او درباره اصلاحات اجتماعی برای حکمرانان قابل قبول نبود و او مجبور شد به
اتفاق مادر و تنها مریدش از جزیره فرار کند.
فیثاغورث
از آنجا به جنوب ایتالیا عزیمت کرد، که در آن زمان بخشی از ماگنا گراسیا (Magna Graecia) بود. او در کروتون (Croton) سکنی گزید و در آنجا مورد حمایت مایلو (Milo) قرار گرفت که ثروتمندترین مرد کروتون، و یکی از
قویترین مردان تاریخ بشمار میرفت. هر چند شهرت فیثاغورث بعنوان حکیم ساموس از قبل
در یونان پیچیده بود، ولی آوازه مایلو حتی از او نیز بیشتر بود. مایلو شباهت زیادی
به هرکول داشت. او قهرمان المپیک بود و دوازده بار نیز قهرمان بازیهای پیتیان (Pythian) شده بود. علاوه بر افتخارات ورزشی، مایلو فلسفه و
ریاضیات نیز خوانده بود و قسمتی از خانه خودش را به فیثاغورث اختصاص داد تا مدرسهای
را در آنجا تاسیس کند. اینجا بود که خلاقترین ذهن و قویترین جسم آن دوران با هم
شراکتی را تشکیل دادند.

تصویری خیالی از فیثاغورث (Pythagoras) و مدرسه او در کوروتون، قرن
ششم ق.م.
فیثاغورث
که در خانه جدید خودش احساس امنیت میکرد انجمن اخوتی را تاسیس کرد که از ششصد نفر
از طرفدارانش تشکیل شده بود. آنها نه فقط میتوانستند آموزههای او را درک کنند،
بلکه میتوانستند با ساختن ایدهها و اثباتهای جدید به غنای آنها بیافزایند.
هنگامی که کسی به انجمن اخوت وارد میشد باید کلیه داراییهای خودش را به یک صندوق
مشترک وقف میکرد و هر کسی که این انجمن را ترک میکرد باید به او دو برابر مقداری
که وقف کرده بود پرداخت میشد و سنگی نیز به یادبود او اختصاص میافت. انجمن اخوت
یک مدرسه تساوی طلب بود، که چند زن نیز در آن حضور داشتند. شاگرد مورد علاقه
فیثاغورث، دختر زیبای خود مایلو، یعنی تیانو (Theano)
بود، و با وجود اختلاف سنی زیاد، آنها سرانجام با یکدیگر ازدواج کردند.
فیثاغورث
کمی پس از تاسیس انجمن برادری واژه ’فیلسوف‘ (philosopher)
را اختراع کرد، و با اینکار هدف مدرسه خودش را تربیت فلاسفه تعریف کرد. روزی
هنگامی که لئون شاهزاده فیلیوس در مسابقات المپیک حضور داشت، از فیثاغورث خواست تا
خودش را برای او توصیف کند. فیثاغورث در جواب گفت ”من یک فیلسوف هستم“، ولی لئون
که تابحال این واژه را نشنیده بود از او خواست که بیشتر توضیح دهد، و فیثاغورث
اینطور جواب داد:
ای
شاهزاده! زندگی را میتوان بخوبی با این بازیهای عمومی مقایسه کرد که جمعیت زیادی
دور هم گرد میآیند. بعضی خواهان کسب مال هستند، و برخی دیگر امید کسب شهرت و
افتخار را دارند. ولی میان آنها تعدادی نیز هستند که فقط برای مشاهد آمدهاند و میخواهند
آنچه را که اینجا میگذرد درک کنند. زندگی نیز همینگونه است. برخی تحت نفوذ عشقِ
مال هستند درحالیکه برخی نیز تحت نفوذ تب دیوانهوار قدرت و سلطه بر دیگران قرار
میگیرند. ولی درمیان آنها کسانی بهترین هستند که خودشان را وقف کشف معنی و منظور
خود زندگی کردهاند. چنین انسانی بدنبال پرده برداشتن از اسرار طبیعت است. من این
انسان را یک فیلسوف مینامم، هر چند انسانی نیست که از همه جهات عاقل باشد، ولی
بعنوان کلید کشف اسرار طبیعت، او میتواند عاشق خرد باشد.
هر چند
بسیاری از آرمانهای فیثاغورث آگاه بودند، ولی هیچ کس خارج از انجمن اخوت از
جزئیات یا وسعت موفقیتهای او اطلاعی نداشت. هر یک از اعضای مدرسه مجبور بودند
سوگند یاد کنند که هرگز هیچ یک از اکتشافات ریاضی خود را با دیگران درمیان
نگذارند. حتی پس از مرگ فیثاغورث یکی از اعضای انجمن اخوت بدلیل افشای چگونگی
ساختن دوازده وجهی منظم از روی پنجضلعیهای منظم و شکستن این سوگند، به دریا
انداخته شد تا غرق شود. دلیل اینکه افسانههایی در مورد انجمن برادری وجود دارد
بیشتر بخاطر طبیعت فوقالعاده سری آنها بوده، و بطور مشابه دلیل اینکه مدارک خیلی
کمی از دستآوردهای ریاضی آنها وجود دارد نیز همین است.
چیزی که
محقق است این است که فیثاغورث مسلکی را بنا نهاد که مسیر ریاضیات را تغییر داد.
انجمن اخوت یک جامعه مذهبی بود و یکی از چیزهایی که آنها پرستش میکردند اعداد بود.
بواسطه درک رابطهای که میان اعداد وجود داشت، آنها به این باور رسیده بودند که میتوانند
اسرار غیرمادی جهان را کشف و خودشان را به خدا نزدیکتر کنند. آنها تمرکز خودشان را
بویژه بر روی مطالعه اعداد شمارشی (یعنی 1، 2، 3، ...) و کسور گذاشته بودند.
از نظر فنی برخی اوقات ما اعداد شمارشی را اعداد صحیح مینامیم، و این اعداد
باضافه کسور (یعنی نسبت میان اعداد صحیح)، رویهم بعنوان اعداد گویا شناخته میشوند.
در میان بینهایت عددی که وجود دارند، انجمن بدنبال اعدادی بود که دارای اهمیت خاصی
بودند، و برخی از این اعداد بسیار خاص ’اعداد کامل‘ (perfect numbers) نامیده میشدند.
بر اساس
اعتقاد فیثاغورث، کامل بودن یک عدد به مقسومعلیههای آن بستگی داشتند (یعنی
اعدادی که بصورت کامل به عدد اولیه بخش میشدند). برای نمونه، مقسومعلیههای 12 عبارتند از 1، 2، 3، 4، و 6. هنگامی که مجموع
مقسومعلیههای یک عدد از خود آن بیشتر شود، به این عدد زاید (excessive) میگویند. بنابراین 12 یک عددِ زاید است،
زیرا مجموع مقسومعلیههای آن 16 میشود. از سوی دیگر هنگامی که مجموع
مقسومعلیههای یک عدد کمتر از خود عدد باشد، آن عدد ناقص (defective) نامیده میشود. بنابراین 10 یک عددِ ناقص است،
زیرا مجموع مقسومعلیههای آن، یعنی 1، 2 و 5 برابر 8 میشود.
در این
میان، مهمترین و نادرترین اعداد آنهایی هستند که مجموع مقسومعلیههای آنها دقیقاً
با خود عدد برابر باشد و چنین اعدادی کامل (perfect) نامیده میشوند. مقسومعلیههای عدد 6 عبارتند از 1، 2، و 3، درنتیجه این عدد
کامل است. عدد کامل بعدی 28 است، زیرا 1 + 2 + 4 + 7 + 14 = 28 .
اعداد 6 و 28 علاوه بر اینکه
برای انجمن اخوت اهمیت ریاضی داشتند، کامل بودن آنها توسط تمدنهای دیگر نیز تصدیق
شده بود. مثلاً آنها میدیدند که هر 28 روز یکبار ماه بدور زمین میچرخد
و یا گفته میشد که خداوند جهان را ظرف 6
روز خلق کرده است. اگوستین قدیس در
کتاب شهر خدا میگوید گرچه خدا میتوانست جهان را در یک لحظه خلق کند، ولی
تصمیم گرفت اینکار شش روز طول کشد تا منعکس کننده کمال جهان باشد. اگوستین قدیس
اعتقاد نداشت که کامل بودن عدد 6 از این جهت است که خدا آن را انتخاب کرده، بلکه معتقد
بود این کمال در ذات خود عدد نهفته است: ’ خود عدد 6 کامل است، نه بدلیل اینکه همه
چیز در شش روز خلق شده، بلکه عکس آن درست است؛ خدا همه چیز را در شش روز خلق کرده چون
این عدد کامل است. و حتی اگر مورد شش روز هم درمیان نبود، باز هم این عدد کامل میماند.‘
هرچه اعداد بزرگتر میشوند، پیدا کردن اعداد کامل در
میان آنها نیز دشوارتر میشود. سومین عدد کامل 496 است، چهارمی 8,128، پنجمی 33,550,336،
و ششمی 8,589,869,056
است. فیثاغورث متوجه شد که همه اعداد کامل علاوه بر اینکه مجموع همه مقسومعلیههای
خودشان هستند، خواص زیبای دیگری نیز دارند. مثلاً اعداد کامل همیشه مجموع یک سری
از اعداد متوالی صحیح هستند. بنابراین ما میبینیم که:
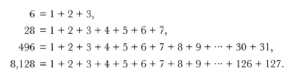
فیثاغورث
اعداد کامل را عزیز میداشت، اما او صرفاً به جمع آوری این اعداد راضی نبود؛ او میخواست
اهمیت درونی آنها را کشف کند. یکی از بصیرتهای او این بود که ’کامل بودن‘ پیوند
نزدیکی با ’دوگانه بودن‘ دارد. ما میدانیم که اعداد 4=2×2، 8=2×2×2، 16=2×2×2×2 ... و غیره، همه توانهایی
از عدد 2
هستند و میتوانند بصورت 2n نوشته شوند، که n نشاندهنده تعداد
دفعاتی است که 2
در خودش ضرب میشود. کلیه این توانهای 2 هیچ وقت کامل نیستند، زیرا مجموع مقسومعلیههای آنها
همیشه از خود عدد یکی کمتر است. این باعث میشود چنین اعدادی ’اندکی ناقص‘
باشند:

دویست سال بعد، اقلیدس ارتباط میان دوگانگی و کمال
را تعریف میکند. اقلیدس درمییابد که اعداد کامل همیشه مضربی از دو عدد هستند که
یکی از آنها توانی از 2 و دیگری توان بعدی 2 منهای 1 است. این یعنی:
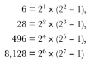
امروزه
جستجو برای یافتن اعداد کامل با استفاده از کامپیوترها ادامه دارد، و ریاضیدانان
توانستهاند اعداد بسیار بزرگی نظیر 2216090× (2216091 – 1) را پیدا کنند که بیش از 130,000 رقم دارد و از قاعده اقلیدس
پیروی میکند.
فیثاغورث شیفته خواص و الگوهای غنی بود که اعداد
کامل دارا بودند و برای ظرافت و جذابیت آنها احترام قائل بود. در نگاه نخست،
امروزه درک مفهوم کامل بودن ساده بنظر میرسد، ولی با این حال یونانیان باستان
قادر نبودند برخی از نکات اساسی مطلب را درک کنند. برای مثال گرچه بسیاری از اعداد
هستند که مجموع مقسومعلیههای آنها از خود عدد یکی کمتر است، و بنابراین میتوانیم
بگوییم آنها اندکی ناقصاند، ولی هیچ عددی نیست که ’اندکی زاید‘ باشد، یعنی مجموع
مقسومعلیههای آن از خود عدد یکی بیشتر باشد. یونانیان نتوانستند چنین عددی را
پیدا کنند، ولی آنها نمیتوانستند دلیل این مسئله را توضیح دهند. هرچند آنها
نتوانسته بودند نمونهای از ’اعداد اندک زاید‘ را پیدا کنند، ولی بدبختانه آنها
نمیتوانستند ثابت کنند که چنین اعدادی وجود ندارند. درک عدم وجود ’اعداد اندک
زاید‘ چیزی نبود که هیچگونه فایده عملی داشته باشد؛ بااینحال این مسئلهای بود که
ممکن بود طبیعت اعداد را توضیح دهد و درنتیجه مطالعه آن ارزشمند باشد. چنین
معماهایی موجب آشفتگی در انجمن اخوت شده بود، و حتی دو هزار و پانصد سال پس از آن
نیز، هنوز ریاضیدانان نتوانستهاند ثابت کنند که اعداد اندک زاید نمیتوانند وجود
داشته باشند.
علاوه بر
مطالعه روابط میان اعداد، فیثاغورث همچنین شیفته ارتباطی بود که میان اعداد و
طبیعت وجود داشت. او میدید که پدیدههای طبیعی از قوانینی پیروی میکنند، و این
قوانین میتوانند بوسیله معادلات ریاضی توصیف شوند. یکی از اولین پیوندهایی که او
کشف کرد، ارتباطی بود که میان هارمونی (هماهنگی) موسیقی و هارمونی اعداد
وجود داشت. مهمترین آلت موسیقی که در زمان یونان باستان وجود داشت چنگ چهارسیم
بود. پیش از فیثاغورث موسیقیدانان میدانستند هنگامی که چنین نُتهایی با هم بصدا
در آیند تاثیر خوبی را ایجاد میکنند، و چنگهای خود را طوری کوک میکردند که وقتی
دو سیم به ارتعاش در میآمدند چنین هارمونی را ایجاد کند. ولی موسیقیدانان باستان
اصلاً درک نمیکردند که چرا نُتهای خاصی با هم همآهنگ بودند و هیچ سیستم علمی
برای کوک کردن سازهای خود نداشتند. در عوض آنها چنگهای خود را تا وقتی صدای
هارمونی ایجاد نشده بود صرفاً با استفاده از گوش دادن کوک میکردند. دانشمندی بنام
Iamblichus که 9 کتاب درباره
فرقه فیثاغورثیان نوشته بود، توضیح میدهد که چگونه فیثاغورث به اصول هارمونی
موسیقی پی برد. او میگوید فیثاغورث برای تحقیق درباره هارمونی به بازار آهنگرها
رفت و متوجه شد وقتی پُتکها همزمان با هم فرود میآیند بیشتر آنها یک صدای همآهنگ
ایجاد میکنند، ولی بعضی از پُتکها نیز صدای ناخوشآیندی از خودشان در میآورند.
او پس از بررسی این پُتکها متوجه شد آنهایی که از خودشان یک صدای همآهنگ ایجاد
میکنند با هم یک رابطه ساده ریاضی دارند، بصورتی که جرمهای آنها کسر سادهای از
یکدیگر هستند. یعنی پُتکهایی که نصف یکدیگر، یا دو سوم یا سه چهارم یک پتک خاص
هستند، همه اصوات هم آهنگی را تولید میکنند. از سوی دیگر پُتکی که هنگام ضربه زدن
صدای ناهمآهنگی را با دیگران ایجاد میکند به سختی با دیگر پُتکها نسبت وزنی
دارد.
فیثاغورث
متوجه شد که چیزی که باعث هماهنگی در موسیقی میشود داشتن نسبتهای عددی ساده است.
دانشمندان درمورد این داستان تردیدهایی دارند، ولی چیزی که بیشتر محقق است این است
که چطور فیثاغورث این نظریه موسیقی وابسته به نسبتها را با بررسی خواص یک تار
برای چنگها بکار برد. اگر یک تار بطور ساده کشیده شود، نُت استانداردی را تولید
میکند که توسط کُلِ طولِ تار مرتعش شده تولید میشود. با ثابت نگاه داشتن تار در
یک نقطه خاص که در طول آن قرار دارد، این امکان وجود دارد تا ارتعاشات یا صداهای
دیگری را تولید کرد. چیزی که اهمیت دارد این است که صداهای هماهنگ تنها در نقاط
بخصوصی ایجاد میشوند. برای مثال با ثابت نگاه داشتن تار در نیمه طول آن، با مرتعش
کردن آن صدایی تولید میشود که یک اوکتاو (octave)
بالاتر است و با صدای اولیه همآهنگی دارد. به طور مشابه، با ثابت نگاه داشتن تار
در نقاطی که دقیقاً در یک سوم، یک چهارم، یا یک پنجم طول تار قرار دارند صداهای همآهنگ
دیگری تولید میشوند. ولی با ثابت نگاه داشتن تار در نقطهای که نسبت سادهای با
طول تار ندارد، صدایی تولید میشود که با دیگر صداها همآهنگی ندارد.
فیثاغورت
برای اولین بار قوانین ریاضی که بر پدیدههای فیزیکی حکمفرما بودند را کشف کرد و
نشان داد که میان علم و ریاضیات یک رابطه اساسی وجود دارد. از آن زمان به بعد
دانشمندان همیشه در جستجوی قواعد ریاضی بودهاند که بنظر میرسد بر روندهای فیزیکی
حاکم هستند و دریافتهاند که اعداد در همه پدیدههای طبیعی ظاهر میشوند. مثلاً
عددی هست که بنظر میرسد در طول رودخانههای پرپیچ و خم دخیل باشد. پرفسور هانس-هنریک
استولم (Hans-Henrik Stølum)، که یک متخصص زمین
شناس در دانشگاه کمبریج است، نسبت میان طول واقعی رودخانهها از دهانه تا منبع و
طول مستقیم آنها را حساب کرده. هرچند این نسبت از یک رود به رود دیگر تغییر میکند،
ولی مقدار میانگین آنها کمی بیشتر از 3 است، یعنی میتوان گفت طول واقعی چیزی حدود سه برابر
طول مستقیم است. درواقع این نسبت تقریباً با 3.14 برابر است، که به مقدار عدد π (نسبت میان محیط و قطر یک دایره) نزدیک است.
عدد π ابتدا در اندازهگیری دایره ظاهر میشود، ولی بعداً
سر و کله آن بارها و بارها در بسیاری از رویدادهای علمی پدیدار میشود. در مورد
نسبت طول رودخانه، ظاهر شدن π نتیجه نبرد
میان نظم و بینظمی است. اینشتین اولین کسی بود که گفت رودخانهها تمایل دارند تا
مسیر خمیده بیشتری داشته باشند، زیرا یک خم کوچک به شدت جریان آب بیشتر منجر میشود،
که به نوبه خودش به فرسایش بیشتر و خمهای تندتر منجر میشود. خم تندتر، جریان
تندتر در لبههای بیرونی، فرسایش بیشتر، پیچش بیشتر رودخانه، و غیره. ولی روند
طبیعی دیگری نیز هست که موجب کاستن از این آشفتگی (chaos) میشود: افزایش پیچشِ رودها موجب میشود تا بر روی
خودشان تا شوند و در حقیقت یک میانبر ایجاد شود. رودخانه مستقیمتر میشود و حلقه
در یکطرف آن باقی میماند تا یک دریاچه Uشکل را ایجاد کند. تعادل میان این دو عاملِ
متقابل به این منجر میشود که نسبت طول واقعی رود به فاصله میان منبع و دهانه آن
برابر با عدد π باشد. این نسبت را میتوان در
بسیاری از رودخانههایی که شیب بسیار ملایمی دارند، مثل آنهایی که در برزیل یا
سیبری جاری هستند مشاهده کرد.
فیثاغورث
متوجه شد که اعداد در همه جا حضور دارند، از هارمونیهای موسیقی گرفته تا مدار
سیارات، و این باعث شد او ادعا کند که ’همه چیزها عدد هستند‘. با اکتشاف در معنی
ریاضیات، فیثاغورث زبانی را توسعه داد که دانشمندان را قادر میساخت طبیعت جهان را
توصیف کنند. از آن به بعد، با هر پیشرفتی که در ریاضیات رخ میداد مجموعه لغات
بیشتری دراختیار دانشمندان قرار میگرفت که آنها میتوانستند برای توصیف بهتر
پدیدههای اطراف خودشان از آنها استفاده کنند. در واقع پیشرفتهایی که در ریاضیات
بوجود میآمد موجب ایجاد تحولاتی در علوم دیگر میشد.
آیزاک
نیوتون علاوه بر کشف قانون جاذبه، یک ریاضیدان قدرتمند نیز بود. بزرگترین سهمی که
او در ریاضیات داشت توسعه حسابان (Calculus)
بود، که سالها بعد فیزیکدانان از آن بعنوان زبانی استفاده کردند که بهتر میتوانست
قوانین جاذبه و حل مسائل مربوط به گرانش را توصیف کند. نظریه گرانشِ کلاسیکِ
نیوتون برای قرنها دست نخورده باقی ماند، تا آنکه نظریه نسبیت عام اینشتین
جایگزین آن شد. نظریه نسبیت عام میتوانست جزئیات بهتر و بیشتری از گرانش ارائه
دهد. نظریات اینشتین تنها به این دلیل امکان بروز داشتند که در زمان او ابزارهای
جدید ریاضی در دست بودند که او میتوانست با استفاده از آنها ایدههای علمی خود را
در قالب زبان پیچیدهتری توصیف کند. امروز نیز تفسیرهایی که از گرانش ارائه میشوند
بار دیگر تحت تاثیر پیشرفتهایی قرار گرفتهاند که اخیراً در ریاضیات حاصل شده.
آخرین نظریات کوانتوم و گرانش بطور تنگاتنگی به توسعه ریسمانهای ریاضی گره خوردهاند.
نظریه ریسمان (strings theory)
نظریهای است که از خواص هندسی و توپولوژیکی لولهها برای توصیف نیروهای طبیعت
استفاده میکند، و فعلاً بنظر میرسد که از همه مناسبتر باشد.
از میان
همه پیوندهایی که میان اعداد و طبیعت وجود دارد، و توسط انجمن اخوت مورد مطالعه
قرار گرفت، مهمترین آنها فرمولی است که نام مخترع آن را بر خود دارد. قضیه
فیثاغورث (Pythagoras’ theorem)
معادلهای را در دسترس ما قرار داده که برای کلیه مثلثهای قائمالزاویه صادق است
و بنابراین اساس تعریف یک مثلث قائمالزاویه است. خود زاویه قائمه (زاویه 90 درجه)، عمود بودن را
تعریف میکند، یعنی رابطهای که میان خط افقی و عمودی وجود دارد، و نهایتاً همین
است که رابطه میان سه بُعدِ جهانِ آشنای ما را تعریف میکند. از طریق زاویه قائمه،
ریاضیات ساختار کلی فضایی که ما در آن زندگی میکنیم را تعریف میکند.
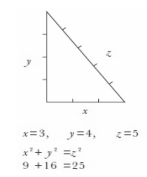
شکل 1- کلیه مثلثهای قائمالزاویه از قضیه فیثاغورث
پیروی میکنند.
با اینکه
ریاضیات لازم برای درک قضیه فیثاغورث نسبتاً ساده است، ولی واقعیت مهمی محسوب میشود.
برای درک آن تنها لازم است دو ضلع یک مثلث قائمالزاویه را اندازه بگیرید (y و x)، و سپس مربعات آنها
را بدست آورید (y2
و x2).
و سپس این دو مربع را با هم جمع کنید (y2 +
x2) تا عدد نهایی حاصل شود.
اگر شما همین عملیات را برای مثلثی که در شکل 1 نشان داده شده انجام دهید، خواهید
دید که جواب 25
است.
حالا شما
میتوانید طول وتر (hypotenuse)
مثلث قائمازاویه را، که با z نشان داده شده،
اندازه بگیرید و مربع آن را حساب کنید. نتیجه قابل توجه این است که این عدد، یعنی z2، با آنچه شما قبلاً
حساب کردید، دقیقاً برابر است (52=25). یعنی میتوان گفت:
در یک
مثلث قائمالزاویه مربع وتر با مجموع مربعات دو ضلع دیگر برابر است.
یا بعبارت
دیگر:
y2 + x2 = z2
این برای
مثلثی که در شکل 1 نشان داده شده بطور وضوح درست است، ولی آنچه مهم است این است که قضیه
فیثاغورث برای هر مثلث قائمالزاویه که شما ممکن است تصور کنید درست است. این یکی
از قوانین عمومی ریاضیات است، و هر موقع شما با یک مثلث قائمالزاویه برخورد کردید
میتوانید بر آن تکیه کنید. برعکس، اگر شما مثلثی را داشته باشید که از قضیه
فیثاغورث پیروی کند، آنگاه میتوانید مطمئن باشید که این مثلث قائمالزاویه است.
در اینجا
باید اشاره کنم که هرچند این قضیه همیشه با نام فیثاغورث پیوند خورده، ولی در واقع
هزار سال قبل از او نیز چینیها و بابلیان از آن استفاده میکردند. ولی چیزی که
این تمدنها نمیدانستند این بود که این قضیه در مورد هر مثلث قائمالزاویهای
(که آنها هرگز آن را هم ندیدهاند) نیز صادق است. دلیل اینکه به این ادعا قضیه
(theorem) گفته میشود این است که
نمونهای از حقایق عمومی است.
ولی آیا
خود فیثاغورث میدانست که این قضیه برای کلیه مثلثهای قائمالزاویه صادق است؟ او
انتظار نداشت بتواند تعداد بینهایتی از مثلثهای قائمالزاویه را برای درستی این
قضیه بررسی کند، ولی بااینحال صد در صد مطمئن بود که این قضیه یک واقعیت مطلق است.
دلیل اطمینان وی نیز به مفهوم اثبات ریاضی تکیه داشت. یافتن یک اثبات ریاضی یعنی
جستجو برای دانشی که از تمام دانشهایی که قبلاً توسط علوم دیگر جمع آوری شده
مطلقتر باشد. چیزی که در طی 2500 سال گذشته موجب انگیزه برای ریاضیدانان بوده،
آرزوی دستیابی به حقیقت غایی از طریق اثبات است.
داستان
آخرین قضیه فرما بر حول جستجو برای یافتن یک اثبات گمشده میگردد. اثبات ریاضی
نسبت به آنچه ما در زبان روزمره خودمان از آن بعنوان اثبات یاد میکنیم، و یا حتی
نسبت به آنچه فیزیکدانان یا شیمیدانان از آن بعنوان اثبات یاد میکنند قویتر و
محکمتر است. تفاوت مهم و ظریفی میان اثبات علمی و اثبات ریاضی وجود دارد، و درک
این تفاوت برای فهم کارهایی که ریاضیدانان از زمان فیثاغورث تابحال انجام دادهاند
بسیار حیاتی است.
اساس یک
اثبات ریاضی کلاسیک با درست شمردن یک سری از اصول موضوعه (axioms) شروع میشود. اصول موضوعه گزارههایی هستند که درست بودن
آنها بدیهی است و میتوان آنها را درست فرض کرد. سپس این امکان وجود دارد که مرحله
به مرحله از طریق استدلال منطقی به یک نتیجه رسید. اگر اصول موضوعه درست باشند و
منطق بکار رفته نیز بینقص باشد، آنگاه نتیجه حاصله غیر قابل انکار خواهد بود.
همین نتیجه غیر قابل انکار است که ما آن را قضیه مینامیم.
قضایای
ریاضی بر این روند منطقی تکیه دارند و هنگامی که اثبات شدند تا ابد صحیح میمانند.
اثباتهای ریاضی مطلقاند. برای اینکه به ارزش چنین اثباتهایی پی ببریم، میتوانیم
آنها را با روابط ضعیفتری، مثل اثباتهای علمی، مقایسه کنیم. در علم برای توضیح یک
پدیده، یک فرضیه (hypothesis)
مطرح میشود. اگر مشاهداتی که در مورد این پدیده صورت میگیرد بخوبی با فرضیه
تطابق داشته باشند، همه اینها فقط شاهدی برای طرفداری از این فرضیه خواهند بود.
بعلاوه، فرضیه صرفاً نباید یک پدیده شناخته شده را توصیف کند، بلکه باید بتواند
نتیجه پدیدههای دیگر را نیز پیشبینی کند. ممکن است برای بررسی قدرتِ فرضیه مورد
نظر بتوان آزمایشاتی را انجام داد، و اگر بطور پیوسته نتایج موفقیت باشند، آنگاه
این نیز شاهدی برای پشتیبانی بیشتر از فرضیه است. نهایتاً ممکن است مقدار شواهد
برای پشتیبانی از فرضیه آنقدر زیاد باشد که آن را بعنوان یک نظریه (theory) علمی قبول کرد.
ولی یک
نظریه علمی هیچگاه نمیتواند در همان سطحِ مطلقِ یک قضیه ریاضی اثبات شود: بلکه
صحت چنین نظریهای بر پایه شواهد موجود بسیار محتمل فرض میشود. اثباتهای بهاصطلاح-علمی،
به مشاهده و ادراک وابستهاند، که هر دو آنها جايزالخطا هستند و تنها تقریبی از
واقعیت را به ما میدهند. برتراند راسل (Bertrand
Russell) میگوید: ”گرچه این ممکن است متناقض بنظر برسد،
ولی کُل علم زیر سلطه ایده تقریب قرار گرفته است“. حتی ’اثباتهای‘ علمی که بطور
گسترده مورد پذیرش قرار گرفتهاند نیز جزء کوچکی از تردید در آنها وجود دارد. برخیاوقات
این تردید تقلیل مییابد، هرچند هیچگاه بکلی ناپدید نمیشود، ولی مواقعی نیز هست
که این اثباتها کاملاً اشتباه از آب در میآیند. ضعفی که در اثباتِ علمی وجود
دارد به انقلابهایی منجر شده که در آنها یک نظریه که قبلاً درست فرض میشده با
نظریه دیگری جایگزین شده، نظریهای که ممکن است فقط اصلاح نظریه قبلی باشد، یا
شاید هم بکلی مغایر آن باشد.
برای
مثال، جستجو برای ذرات بنیادی ماده که توسط نسلهای مختلفی از فیزیکدانان انجام
گرفته، هرکدام نظریات نسلهای قبلی را واژگون، یا حداقل آنها را بطور اساسی اصلاح
کرده. تلاشهای نوین برای یافتن اجزاء سازنده جهان هنگامی رخ داد که در ابتدای قرن
نوزدهم جان دالتون با آزمایشاتی که انجام داد به این نتیجه رسید که هر چیزی
از اتمهای مجزایی ساخته شده، و این اتمها اجزاء بنیادی جهان هستند. در پایان قرن
نوزدهم اولین ذره زیراتمی، یعنی الکترون، توسط جی. جی. تامپسون کشف شدد و
از آن به بعد دیگر اتم یک چیز بنیادی بحساب نمیآمد. در طول سالهای اولیه قرن
بیستم، فیزیکدانان تصویری ’کامل‘ از اتم ارائه دادند، که شامل هستهای بود که از
پروتونها و نوترونها تشکیل شده بود، و الکترونها بدور آن میچرخیدند. برای
چندین سال پروتونها، نوترون، و الکترونها با سرفرازی اجزاء سازنده جهان را تشکیل
میدادند. پس از آن آزمایشات مربوط به پرتوهای کیهانی (cosmic ray) وجود ذرات بنیادی دیگری را
آشکار کردند که پیون (pion) و موئون (muon) نام داشتند. حتی در سال 1932 با کشف ذرات پادماده
(antimatter)، یعنی پادالکترون،
پادپروتون، پادنوترون، و غیره، انقلاب مهمتری رخ داد. در این زمان فیزیکدانها
دیگر نمیتوانستند مطمئن باشند که چه ذرات دیگری میتوانند وجود داشته باشند، ولی
حداقل مطمئن بودند که هیچ یک از این ذرات بنیادی نبودند. این وضعیت ادامه داشت، تا
اینکه در دهه 1960 مفهوم کوارک (quark)
زاده شد. ظاهراً پروتون، نوترون و پیون خودشان از کواکهایی تشکیل شدهاند که
بارهای کسری دارند. نتیجه اخلاقی داستان این است که اگر نگوییم فیزیکدانان هر دم
تصویر خودشان از جهان را پاک کرده و تصویر دیگری را رسم میکنند، ولی باید گفت
دائماً مشغول تغییر دادن این تصویر هستند. در دهههای آتی حتی ممکن است مفهوم
ذراتی که به شکل اشیاء نقطهای هستند با ایده ذراتی که به شکل ریسمان
(string) هستند جایگزین شوند – همان
ریسمانهایی که ممکن است بهترین راه برای توصیف گرانش نیز باشند. این نظریه میگوید
که طول ریسمانها یک میلیاردیم یک میلیاردیم یک میلیاردیم یک میلیاردیم یک متر است
(بقدری کوچک که مانند یک نقطه بنظر میرسند). آنها میتوانند به طرق مختلفی مرتعش
شوند، و نتیجه هر کدام از این ارتعاشات به ذره متفاوتی میانجامد. این مشابه همان
کشف فیثاغورث است که میگفت تارهای یک چنگ بر حسب ارتعاش خودشان میتوانند صداهای
گوناگونی را تولید کنند.
آرتور
سی کلارک (Arthur C. Clarke)، که نویسنده داستانهای علمی-تخلیی و یک
آیندهشناس بود، درجایی میگوید ’اگر یک استاد برجسته علوم بگوید فلان چیز بدون شک
درست است، آنگاه محتمل است که روز بعد ثابت شود که آن چیز غلط است. اثبات علمی به
ناچار بیثبات و سست است. از سوی دیگر اثبات ریاضی مطلق و عاری از تردید است.‘
فیثاغورث درحالی مرد که مطمئن بود قضیه او، که در دو هزار پانصد سال گذشته صحیح
بوده، تا ابد نیز صحیح خواهد ماند.
علم بر اساس یک سیستم قضایی عمل میکند. یک نظریه
فقط تا وقتی صحیح است که هیچ نظریه دیگری ارائه نشده باشد که خلاف آن را
نشان دهد. از سوی دیگر ریاضیات چیزی نیست که بر شواهدی تکیه داشته باشد که حاصل
آزمایشات خطاپذیر هستند، بلکه بر منطق تکیه دارد که خطاناپذیر است. این را میتوان
توسط مسئله ’صفحه شطرنج ناقص‘ (mutilated
chessboard) نشان داد که در شکل 2 نمایش داده شده.

شکل 2- مسئله صفحه شطرنج ناقص و دومینویی که در زیر آن
نشان داده شده.
در اینجا
ما یک صفحه شطرنج را داریم که دو گوشه قطری آن برداشته شده، بنابراین بجای 64
خانه، 62 خانه دارد. حالا ما 31 دومینو را برمیداریم، طوری که هر دومینو دقیقاً دو
خانه را بپوشاند. مسئله این است: آیا امکان دارد با 31 دومینو بتوان تمام 62 خانه این صفحه شطرنج
را پوشش داد؟
دو رویکرد
برای حل این مسئله وجود دارد:
(1) رویکرد علمی
یک
دانشمند سعی میکند این مسئله را توسط انجام آزمایش حل کند، و پس از اینکه چند
چیدمان را امتحان کرد، به این نتیجه میرسد که همه آنها با شکست ربرو میشوند.
نهایتاً دانشمند به این نتیجه میرسد که آنقدر مدرک در دست دارد که بگوید ’نمیتوان
صفحه را به این صورت پر کرد‘. ولی دانشمند هرگز نمیتواند مطمئن باشد که این نتیجهگیری
مطلقاً صحیح است، زیرا ممکن است چیدمانی وجود داشته باشد که او آن را امتحان نکرده
و بتواند صفحه را پوشش دهد. برای اینکار میلیونها چیدمان مختلف وجود دارد که تنها
میتوان بخش کوچکی از آنها را بررسی کرد. نتیجه اینکه چنین کاری غیر ممکن است،
ارائه یک نظریه است که برپایه آزمایش قرار دارد، ولی دانشمند باید انتظار روزی
را داشته باشد که ممکن است نظریه او واژگون شود.
(2) رویکرد ریاضی
ریاضیدان
سعی میکند با طرح یک استدلال منطقی به این سئوال پاسخ دهد، و آنچه نهایتاً حاصل میشود
بدون تردید صحیح خواهد بود و تا ابد بدون تغییر خواهد ماند. استدلال ریاضی ما
بصورت زیر است:
· آن گوشههایی از صفحه شطرنج که ناقص هستند
هر دو سفیدند. بنابراین ما حالا 32 خانه سیاه و 30 خانه سفید داریم.
· هر دومینو میتواند دو خانه مجاور هم را پوشش
دهد، و خانههای مجاور همیشه رنگهای متفاوتی دارند، که یکی سفید و دیگری سیاه
است.
· بنابراین به هر طریقی که دومینوها چیده
شوند، 30
دومینو اولی که بر روی صفحه قرار میگیرند باید 30 خانه سفید و 30 خانه سیاه را
بپوشانند.
· در نتیجه در آخر کار برای شما یک دومینو و
دو خانه سیاه باقی خواهد ماند.
· ولی بخاطر دارید که کلیه دومینوها فقط خانههای
مجاور هم را میپوشانند، و خانههای مجاور دارای رنگ متفاوتی هستند. ولی دو خانه
باقیمانده هر دو سیاه هستند و در نتیجه در کنار هم قرار ندارند تا توسط یک دومینو
پوشانده شوند. پس پوشاندن این صفحه با دومینو غیر ممکن است!
این اثبات
نشان میدهد که هر چیدمانی از دومینوها برای پوشاندن صفحه شطرنج ناقص نهایتاً با
شکست روبرو میشود. بطور مشابه، فیثاغورث نیز قضیهای را اثبات کرد که نشان میدهد
تمام مثلثهای قائمالزاویه از یک قاعده پیروی میکند. مفهوم اثبات ریاضی برای
فیثاغورث مقدس بود، و این اثبات بود که انجمن اخوت را قادر ساخت دستاوردهای بیشتری
حاصل کنند. بیشتر اثباتهای ریاضی امروزی بسیار پیچیده هستند، طوری که دنبال کردن
منطقی که در پشت آنها قرار دارد برای یک فرد غیر متخصص غیر ممکن است. ولی
خوشبختانه برای قضیه فیثاغورث این استدلال نسبتاً ساده است و تنها به ریاضیات
دبیرستانی تکیه دارد. برهانِ (یا بعبارتی اثباتِ) فیثاغورث غیر قابلانکار است.
این نشان میدهد که قضیه او برای تمام مثلثهای قائمالزاویه جهان صادق است. کشف
این اثبات چنان اهمیت داشت که صد گاو نر برای شکرگذاری از خدایان قربانی شدند. این
کشف رویداد شاخصی در ریاضیات، و یکی از مهمترین پیشرفتها در تاریخ تمدن بشر محسوب
میشود. اهمیت آن دوچندان است. اول اینکه باعث شد ایده اثبات گسترش یابد. اگر یک
نتیجهگیری ریاضی به اثبات رسیده باشد، چون این اثبات نتیجه یک منطقِ گام به گام
است، از هر حقیقت دیگری عمیقتر است. هر چند فیلسوفی بنام طالس برخی از اثباتهای
هندسی را پیش از فیثاغورث اختراع کرده بود، ولی این فیثاغورث بود که این ایده را
بسیار جلوتر برد و توانست گزارههای ریاضی بِکری را اثبات کند. دومین برآمد قضیه
فیثاغورث این است که روشهای مجرد ریاضی با چیزی پیوند داده میشوند که ملموس است.
فیثاغورث نشان داد که حقیقت ریاضی میتواند در مورد جهان علمی بکار گرفته شود و
برای آن یک اساسِ منطقی فراهم آورد. ریاضیات پایه محکمی را در اختیار علم قرار میدهد
و دانشمندان بر اساس این پایهِ لغزشناپذیر، اندازهگیریهای غیر دقیق و مشاهدات
ناقص خودشان را انجام میدهند.
با
اشتیاقی که انجمن اُخوت فیثاغورث برای جستجوی حقیقت توسط اثبات داشتند، بر غنای
ریاضیات افزودند. خبر موفقیت آنها در همه جا پیچید ولی جزئیات اکتشافات آنها سرّی
باقی ماند. خیلیها برای ورود به این حریمِ مقدسِ دانش درخواست میدادند، ولی از
میان آنها تنها بااستعدادترین اشخاص پذیرفته میشدند. در میان کسانی که تقاضای
آنها رد شد کسی بنام سایلون (Cylon)
بود. سایلون به جهت عدم پذیرش تحقیرآمیزش کینه بدل گرفت، و بیست سال بعد انتقام
خودش را گرفت.
در شصت و
هفتمین دوره مسابقات المپیک (در سال 510 قبل از میلاد) در شهر مجاور، که سیباریس
نام داشت، شورشی اتفاق افتاده بود. رهبر شورشیان که تلیز نام داشت، شروع به تعقیب
وحشیانه طرفداران دولت سابق کرد، و بسیاری از آنها به کروتون پناه بردند. تلیز
خواستار شد که خائنین به سیباریس بازگردانده شوند تا در آنجا مجازات شوند. ولی
مایلو و فیثاغورث شهروندان کروتون را ترغیب کردند تا در برابر این رهبر ظالم
ایستادگی کنند و از پناهندگان پشتیبانی کردند. تلیز از این اقدام خشمگین شد و
فوراً ارتشی متشکل از 300 هزار نفر را جمع آوری کرد و بسوی کروتون رهسپار شد. در
آنجا مایلو با ارتشی که از 100 هزار نفر غیرنظامی تشکیل شده بود از شهر دفاع کرد.
پس از گذشت هفتاد روز، رهبری خوب مایلو او را به پیروزی رساند و او برای تلافی،
مسیر رودخانه کاراتیس را بسوی سیباریس تغییر داد تا آن شهر توسط سیل ویران شود.
بحث درباره اینکه باید با عنائم چه کرد در جریان بود، و به همین دلیل باوجود اینکه
جنگ به پایان رسیده بود هنوز شهر کروتون در آشوب بود. شهروندان عادی کروتون از این
بیم داشتند که این غنائم به نخبگان انجمن اخوت فیثاغورث داده شود، و به همین جهت
شروع به اعتراض کردند. بدلیل اینکه انجمن اخوت کشفیات خود را مخفی نگاه میداشت،
از قبل هم مردم کدورتهایی را از فیثاغورثیان بدل داشتند. ولی تا وقتی سایلون
بعنوان صدای مردم ظاهر نشده بود این اعتراضات به جایی نرسیده بود. چیزی که سایلون
بر روی آن حساب بازکرده بود ترس، سوءظن، و رشک مردم خشمگین بود. این باعث شد تا او
رهبری ماموریتی را در دست بگیرد که هدف آن نابودی باشکوهترین مدرسه ریاضی بود که
جهان تا بحال بخود دیده بود. خانه مایلو و مدرسهای که در مجاورت آن قرار داشت
محاصره شد، کلیه درها قفل شدند و برای جلوگیری از فرار، پشت آنها مانعهایی قرار
داده شد. سپس آتش زدن شروع شد. مایلو توانست با مبارزه از این دوزخ بگریزد، ولی
فیثاغورث به همراه بسیاری از مریدانش در این آتش سوزی کشته شدند.
ریاضیات
اولین قهرمان بزرگ خود را از دست داده بود، ولی روح فیثاغورثی زنده ماند بود.
اعداد و حقایقی که در پشت آنها قرار دارند جاودانهاند. فیثاغورث نشان داد که بیش
از هر رشته دیگری، ریاضیات موضوعی است که ذهنی نیست. مریدان او نیازی نداشتند تا
استادشان درباره معتبر بودن یک نظریه خاص اظها نظر کند. درستی یک نظریه مستقل از
نظر دیگران بود. در عوض، این ساخت منطق ریاضی بود که به داور تبدیل شد.
فیثاغورثیان روشی برای حاصل کردن حقیقت از خودشان بجا گذاشتند، حقیقتی که فراتر از
خطاپذیری حکم انسان بود، و این بزرگترین سهمی بود که آنها در تمدن داشتند.
بدنبال
حمله سایلون و کشته شدن موسس انجمن فیثاغورثیان، آنها کروتون را به مقصد ماگنا
گریسیا ترک کردند، ولی آزار آنها ادامه یافت و نهایتاً بسیاری از آنها در جزایر
خارجی سکنی گزیدند. این تبعید اجباری فیثاغورثیان را مجبور کرد تا دانش ریاضی خود
را در سراسر جهانِ کهن پخش کنند. شاگردان فیثاغورث مدارس جدیدی را تاسیس کردند و
روش استدلال منطقی را به شاگردان خود آموزش دادند. علاوه بر اثبات قضیه فیثاغورث،
آنها روش پیدا کردن اعدادی را فاش کردند که به سهگانههای فیثاغورثی
(Pythagorean triples) معروف هستند.
سهگانههای
فیثاغورثی ترکیبی از سه عدد صحیح هستند، که بطور کامل در معادله فیثاغورث (یعنی x2 + y2
= z2) صدق میکنند. مثلاً اگر x=3، y=4، و z=5 باشند، این معادله برقرار است:
32 + 42
= 52, 9 + 16 = 25
طور دیگری
که میتوان سهگانههای فیثاغورثی را درنظر گرفت به روش بازچینی دوباره مربعها
است. اگر یکی از مربعها 3 × 3 باشد که از 9 مربع واحد تشکیل شده، و دیگری یک مربع 4 × 4 باشد که از 16 مربع واحد
تشکیل شده، آنگاه همانطور که در شکل 3 نشان داده شده، میتوان آنها را طوری
بازچینی کرد که یک مربع 5×5 را تشکیل دهند.
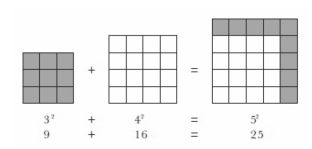
شکل 3. پیدا کردن اعداد صحیحی که در معادله
فیثاغورث صدق میکنند را میتوان بصورت یافتن دو مربع در نظر گرفت که میتوانند
برای تشکیل یک مربع سوم با هم جمع شوند. برای مثال مربعی که از 9 مربع واحد تشکیل شده
باشد میتواند با مربعی که از 16 مربع واحد تشکیل شده جمع شود، و روی هم مربعی را تشکیل
دهند که از 25
مربع واحد تشکیل شده است.
فیثاغورثیان
میخواستند سهگانههای دیگری را پیدا کنند. یعنی مربعهایی را پیدا کنند که وقتی
با هم جمع میشوند، مربع سومی را تشکیل دهند که از آن دو بزرگتر بود. یک نمونه
دیگر از سهگانههای فیثاغورثی بصورت x=5، y=12،
و z=13 است:
52
+ 122 = 132,
25 + 144 = 169
یک سهگانه
دیگر فیثاغورثی بصورت x=99،
y=4,900، و z=4,901 است. همانطور که
اعداد بزرگتر میشوند، سهگانههای فیثاغورثی نیز کمیابتر میشوند، و یافتن آنها
سختتر میشود. فیثاغورثیان یک روش باقاعده پیدا کردند که تا آنجا که امکان داشته
باشد، میتوان از آن برای یافتن سهگانههای فیثاغورثی استفاده کرد، و بکارگیری
این روش نشان میدهد که تعداد بینهایتی از سهگانههای فیثاغورثی وجود دارند.
نام کتابی
که وایلز از کتابخانه عمومی قرض گرفت و توجه او را جلب کرد، آخرین مسئله
بود، که در آن قضیه فیثاغورث و وجود تعداد بینهایت سهگانهها شرح داده شده
بود. هرچند انجمن اخوت تقریباً به درک کاملی از سهگانههای فیثاغورثی دست یافته
بود، وایلز جوان متوجه شد که این معادله بظاهر ساده x2 + y2
= z2 سوی تاریکی نیز دارد. این کتاب وجود یک
حقیقت ریاضی هولناک را نیز شرح داده بود.
در معادله
فیثاغورث هر سه عدد x، y، و z بصورت مربع با هم جمع
شدهاند.
x2 + y2 = z2
ولی در آن
کتاب معادله مشابهی نیز آمده بود که در آن مکعب اعداد با هم جمع شده بود. در این
معادله، توان x دو نیست، بلکه سه
است:
x3 + y3 = z3
هنگامی که
توان 2
باشد، یافتن اعداد صحیحی که در معادله x2 + y2=z2
صدق کنند (که همان سهگانههای فیثاغورثی باشند) کار نسبتاً سادهای است. ولی با
تغییر توان از 2
به 3 (تغییر مربع به مکعب)، غیر ممکن است که بتوان سه عدد صحیح را پیدا کرد که
در این معادله جدید صدق کنند. ریاضیدانان قرنها تلاش کردند اعداد صحیحی را پیدا
کنند که در این معادله صدق کنند، ولی همه این تلاشها با شکست روبرو شد.
در معادله
’مربعی‘ چالش اصلی این بود که مربعهای کوچکی که در دو مربع جای گرفته بودند طوری
در کنار هم قرار داده شوند تا مربع سومی را تشکیل دهند که از آن دو بزرگتر بود. در
نسخه ’مکعبی‘ چالش این است که بلوکهای سازنده دو مکعب را طوری در کنار هم قرار
داد تا مکعب سومی را تشکیل دهند که از آن دو بزرگتر باشد. اصلاً مهم نیست کارتان
را با چه مکعبهایی شروع میکنید، هر طوری هم آنها را درکنار هم قرار دهید، باز هم
پس از ساختن مکعب سوم، یا بلوکهایی اضافه میآیند، یا یک مکعب ناقص را خواهید
داشت. نزدیکترین حالتی که تابحال کسی توانسته بلوکها را در کنار هم قرار دهد حالتهایی
است که یا یک بلوک زیاد میآید یا یک بلوک کم. برای مثال اگر ما کار خودمان را با x=6، و y=8 شروع کنیم، و بلوکهای دو مکعب را بازچینی کنیم، آنگاه
همانطور که در شکل 4 نشان داده شده، برای ساختن یک مکعب 9 × 9 × 9،
یک بلوک کم میآوریم.
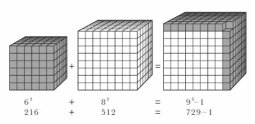
شکل 4. میتوان بلوکهای سازنده دو مکعب را با هم جمع
کرد، ولی آیا میتوان از آنها یک مکعب کامل دیگر ساخت؟ در اینحالت اگر یک مکعب 6 × 6 × 6
به یک مکعب 8 × 8
× 8 اضافه شود، آنها رویهم آنقدر بلوک واحد نخواهند
داشت تا یک مکعب 9
× 9 × 9 را شکل دهند. در اینجا در اولین مکعب 216 (یا 63) بلوک، و در مکعب دوم
512
(83)
بلوک هستند. مجموع بلوکها 728 است که از 93 یکی کمتر است.
بنظر میرسد
یافتن سه عدد صحیح که در نسخه مکعبی معادله (یعنی x3 + y3 = z3)
صدق کنند کاملاً غیر ممکن است. علاوهبراین، اگر توان از 3 به هر توان بالاتری تغییر کند
(مثلاً 4, 5, 6,
…)، آنگاه بنظر میرسد باز هم حل این معادله غیر ممکن است. ظاهراً
معادله عمومی زیر هیچ جوابی ندارند که جزء اعداد صحیح باشند، مگر اینکه n با 2 برابر باشد.
xn + yn = zn
(2 بزرگتر از هایn برای)
اگر ما در معادله فیثاغورث، 2 را با هر عدد بزرگتری جایگزین کنیم، یافتن اعداد صحیحی که در این معادله صدق کنند از یک کار نسبتاً ساده به یک کار بسیار بغرنج بدل میشود. در واقع ریاضیدان قرن هفدهم فرانسوی، پییر دو فرما (Pierre de Fermat) ادعای شگفتانگیزی را در اینمورد مطرح کرد. او گفت دلیل اینکه کسی نتوانسته چنین جوابهایی را پیدا کند این است که اصلاً این معادلات هیچ جوابی ندارند.
فرما یکی از برجستهترین ریاضیدانان تاریخ ریاضیات
بود. او برای بررسی جوابهای این معادله نمیتوانست تعداد بینهایتی از اعداد را
امتحان کند، ولی کاملاً مطمئن بود که هیچ ترکیب سهگانهای از اعداد وجود ندارند که
در معادله مذکور صدق کنند. اطمینان او هم برپایه استدلال قرار داشت. مانند
فیثاغورث که برای نشان دادن صحت قضیه خودش لازم نبود کلیه مثلثهای جهان را امتحان
کند، برای فرما هم لازم نبود کلیه اعداد را امتحان کند تا صحت قضیه خودش را نشان
دهد. چیزی که امروزه به نام آخرین قضیه فرما (Fermat’s Last Theorem) مشهور است میگوید که:
xn+yn=zn معادله
برای nهای بزرگتر از 2،
هیچ جوابی ندارد که n
یک عدد صحیح باشند.
همانطور
که وایلز فصول کتاب بِل را یک به یک میخواند، او متوجه میشد که فرما چقدر شیفته
کارهای فیثاغورث شده بود، و نهایتاً او تصمیم میگیرد به مطالعه شکل تحریف شده
معادله فیثاغورث بپردازد. سپس وایلز با ادعای فرما روبرو میشود که میگوید ’اگر
تمام ریاضیدانان جهان تا ابد در جستجوی جوابی برای معادله فوق باشند، نهایتاً هیچ
جوابی را پیدا نخواهند کرد‘. او باید صفحات این کتاب را با اشتیاق ورق زده باشد،
تا طعم اثبات آخرین قضیه فرما را بخوبی حس کند. ولی در آن کتاب اثباتی برای این
قضیه نیامده بود. بِل کتاب خودش را با گفتن یک جمله به پایان برد و آن این
بود: ’این اثبات خیلی وقت پیش گم شده‘. در آنجا هیچ اشارهای به اینکه این اثبات
چه میتواند باشد نشده بود. وایلز گیج، عصبانی، و خیلی کنجکاو شده بود. البته او
تنها کسی نبود که چنین احساساتی را داشت.
برای بیش
از 300 سال بسیاری از بزرگترین ریاضیدانان جهان سعی کردند تا اثبات گمشده فرما را
بازیاب
ند و در
این راه شکست خوردند. هر چه نسلهای قبل در اینکار ناکام میماندند، نسلهای بعدی
خشمگینتر، و حتی برای حل این مسئله مصممتر میشدند. حدود 100 سال پس از درگذشت
فرما، در سال 1742 ریاضیدان سوئیسی لئونارد اویلر (Leonhard Euler) از دوست خودش که در فرانسه
بود خواست که خانه فرما را جستجو کند تا شاید کاغذهایی که مربوط به این قضیه بود
را پیدا کند. هیچ اثری از اینکه اثبات فرما چه میتوانست باشد پیدا نشد. ما در فصل
2 به شخصیت مرموز پییر دو فرما و اینکه چگونه قضیه او گم شد باز خواهیم گشت، ولی
فعلاً کافیست به گفتن این نکته بسنده کنیم که آخرین قضیه فرما برای قرنها
ریاضیدانان را اسیر خودش کرده بود، و همین مسئله بود که اندو وایلز جوان نیز اسیر
آن شد.
جایی در
کتابخانه عمومی میلتونهیل یک پسر بچه ده ساله نشسته بود و به بدنامترین مسئله
ریاضیات خیره شده بود. معمولاً نیمی از دشواری یک مسئله ریاضی در فهمِ درست آن
است، ولی این مسئله بسیار ساده بود – ثابت کنید اگر n بزرگتر از 2 باشد، معادله xn + yn = zn هیچ جوابی ندارد که
عدد صحیح باشد. اندرو از
اینکه میدید درخشانترین نوابغ جهان در بازیابی اثبات این قضیه ناکام ماندهاند
هراسی بخود راه نداد. در عوض او فوراً با استفاده از تکنیکهایی که از کلاس ریاضی
با آنها آشنا بود درمورد این مسئله شروع بکار کرد و سعی کرد اثبات گم شده را
بازیابد. وایلز پیش خودش فکر میکرد که شاید او میتوانست چیزی را پیدا کند که کسی
جز فرما به ذهنش خطور نکرده بود. او رویای این را داشت که بتواند روزی جهان تکان
دهد.
سیسال
بعد اندرو وایلز برای اینکار آماده بود. او که در تالار بزرگ موسسه ایزک نیوتون
ایستاده بود، بر روی تخته سیاه چیزهایی را نوشت، و درحالی که سعی داشت تا خوشحالی
خودش را پنهان کند، رو به حضار کرد. سخنرانی به اوج خودش رسیده بود و حضار این را
میدانستند. چند تن از آنها بطور پنهانی دوربینهایی را به داخل آورده بودند و
هنگامی که او سخنان پایانی خود را بیان میکرد نور فلاش دوربین تالار را فراگرفته
بود.
او با گچی
که در دستانش بود برای آخرین بار رو به تخته ایستاد. چند خط آخری، اثبات را تکمیل
کرده بودند. در طول بیش از سیصد سال گذشته، این اولین بار بود که چالش فرما
برآورده شده بود. فلاش چند دوربین چشمک زدند تا این لحظه تاریخی را ضبط کنند.
آخرین چیزی که وایلز بر روی تخته نوشت ’آخرین قضیه فرما‘ بود، و سپس رو به حضار
کرد و با فروتنی گفت ’فکر کنم اینجا باید سخنان خودم را تمام کنم.‘
به ناگهان
دویست ریاضیدانی که در تالار حضور داشتند غرق در شادی شدند و صدای کف زدنهای آنها
در فضا پیچید. حتی آنهایی که انتظار چنین نتیجهای را هم داشتند پوزخند میزدند.
پس از گذشت سه دهه اندرو وایلز به رویای خودش دست یافته بود، و بعد از هفت سال
انزوا توانسته بود محاسبات سّری خودش را برملا کند. ولی درحالی که افراد حاضر در
موسسه نیوتون غرق در شادی بودند، مصیبت پنهانی در راه بود. همانطور که وایلز از
این لحظات لذت میبرد، او به همراه بقیه افراد حاضر نمیدانستند که خوفی در کمین نشسته.

پییر دو فِرما (Pierre
de Fermat) 1665-1601
پییر دو فِرما
در 20 آگوست سال 1601 در شهر Beaumont-de-Lomagne
در جنوب فرانسه زاده شد. پدر فرما، دومنیک فرما، یک تاجر ثروتمند چرم بود،
بنابراین پییر آنقدر خوششانس بود تا از تحصیلات خوبی در صومعه فرانسیسکان
گراندسلو، و بدنبال آن در دانشگاه تولوز برخوردار شود. هیچ مدرکی در دست نیست که
نشان دهد فرما در جوانی استعداد خاصی در ریاضیات از خودش بروز داده باشد.
فشارهایی
که از طرف خانواده بر فرما وارد آمد او را وادار کرد که شغلی در زمینه خدمات دولتی
اتخاذ کند، و در سال 1631 به سمت مستشار دادگستری تولوز منصوب شد. اگر
ساکنان محل میخواستند عریضهای را برای شاه و یا دیگر مقامات بلندپایه
بفرستند، ابتدا باید فرما یا یکی از همکارانش را راضی میکردند که درخواستشان حائز
اهمیت است. مستشاران نقش مهمی در ارتباط استانها با پایتخت داشتند. علاوه
بر ارتباط مردم محلی و پادشاه، مستشاران اطمینان پیدا میکردند که فرامین پادشاه
که از پاریس صادر میشد به درستی در نواحی محلی اجراء میشدند. فرما کارمند
باکفایتی بود که از هر نظر وظایف خود را با دلسوزی و با ملاحظه انجام میداد.
کار دیگر
فرما خدمات قضایی بود و مقام او آنقدر بالا بود که در بیشتر امور مهم درگیر شود.
نامهای از ریاضیدان انگلیسی سِر کنلم دیگبی (Sir Kenelm Digby) بجا مانده که این ویژگی فرما
را نشان میدهد. دیگبی در نامهای که به دوست مشترکشان جان والیس (John Wallis) مینویسد، شرح میدهد که
فرما بعلت مشغله کاری درخواست ملاقات با او را رد کرده.
فرما بطور مرتب با دیگبی و والیس مکاتبه داشت. ما بعداً خواهیم دید
که برخی از این نامهها زیاد هم دوستانه نبودند، ولی آنها نشانههایی از زندگی
روزمره فرما، و از جمله کارها ریاضی او را برای ما فراهم میکنند.
فرما
سریعاً در کار خود پیشرفت کرد و بصورت عضوی از نخبگان جامعه درآمد، و از آن موقع
بود که او میتوانست از لقب دو (de)
بعنوان بخشی از نامش استفاده کند. ترفیع او لزوماً حاصل جاهطلبی نبود، بلکه بیشتر
به سلامتی او مربوط بود. در آن زمان طاعون بیشتر اروپا را گرفته بود، و آنهایی که
زنده ماندند ارتقاء مقام گرفتند تا جای آنهایی که مرده بودند را پرکنند. حتی فرما
نیز در سال 1652 به طاعون مبتلا شد، و بیماری او چنان شدید بود که دوستش برنارد
مدون خبر مرگ او را برای چند تن از دوستانش فرستاد. ولی اندکی بعد او این خبر
را تکذیب کرد.
علاوه بر
مخاطراتی که از نظر سلامتی در فرانسه قرن هفدهم وجود داشت، فرما باید از نظر سیاسی
نیز جان سالم بدر میبرد. انتصاب او بعنوان پارلمان تولوز درست سه سال بعد از آن
رخ داد که کاردینال ریشیلیو (Cardinal Richelieu)
بعنوان نخست وزیر فرانسه انتخاب شده بود. این دوران پر از فتنه و دسیسه بود، و هر
کسی که درگیر امور دولتی بود، حتی در سطح محلی نیز، باید مراقب میبود تا به دام
دسیسههای کاردینال نیافتد. فرما این راه را انتخاب کرد سرش بکار خودش باشد و
وظایفش را به بخوبی انجام دهد. او از نظر سیاسی زیاد جاهطلب نبود، و نهایت تلاشش
را میکرد که از جنجالهای پارلمان دور بماند. او در عوض تمام وقت آزادش را صرف
ریاضیات میکرد و سرگرمی او این بود. فرما یک ریاضیدان آماتور واقعی بود،
مردی که اریک تمبل بِل به او لقب ’شاهزاده آماتورها‘ را داده بود. ولی استعدادهای
او چنان قوی بود که وقتی جولیان کولیج (Julian Coolidge)
کتاب آماتورهای بزرگ ریاضی را نوشت، در آن کتاب نامی از فرما نبرد، زیرا
معتقد بود که ’فرما چنان قوی بود که باید او را در ردیف حرفهایها قرار داد.‘
در آغاز
قرن هفدهم، ریاضیات مشغول احیای خودش از دوران تاریک بود و هنوز هم موضوعی نبود که
زیاد محترم شمرده شود. ریاضیدانان نیز آنقدرها مورد احترام نبودند و بیشتر آنها
مجبور بودند خودشان هزینه تحصیلاتشان را تامین کنند. برای مثال گالیله نتوانست در
رشته ریاضی در دانشگاه پیزا تحصیل کند و مجبور شد معلم خصوصی بگیرد. تنها نهادی که
حقیقتا در اروپا بطور فعال ریاضیدانان را تشویق به تحصیل در این رشته میکرد
دانشگاه آکسفورد بود که در سال 1619 کرسی هندسه در آن تاسیس شده بود. اگر بگوییم
که بیشتر ریاضیدانان قرن هفدهم آماتور بودند، این حرف درستی است. ولی فرما مورد
خیلی خاصی بود. او که به دور از پاریس زندگی میکرد، از جامعه کوچک ریاضیدانانی که
در آن زمان در فرانسه وجود داشت جدا بود، کسانی مانند پاسکال (Pascal)، گاسندی (Gassendi)،
و مخصوصاً کشیشی بنام مارین مرسن (Marin
Mersenne).
سهم کشیش
مرسن در نظریه اعداد اندک بود ولی بااینحال نقش مهمی را در ریاضیات قرن-هفدهم بازی
میکند. مرسن پس از پیوستن به سِلک راهبان به مطالعه ریاضیات پرداخت و بعداً همین
موضوع را به راهبان دیگر صومعه آموزش داد. هشت سال بعد او به پاریس نقل مکان کرد.
مرسن بناچار در آنجا با ریاضیدانان دیگر ملاقات کرد، ولی او از بیمیلی آنها برای
صحبت کردن با خودش یا با دیگران ناراحت بود.
آنچه به
طبع اسرارآمیز ریاضیدانان پاریسی میافزود، یک سُنت بود که از قرن شانزدهم بجا
مانده بود. در آن زمان کسانی بودند که کوسیست (cossists) نامیده میشدند و در کار محاسبه مهارت داشتند. آنها
توسط تاجران و بازرگانان استخدام میشدند تا مسائل پیچیده مالی را حل کنند. نام
آنان از واژه ایتالیایی کوسا (cosa)،
به معنی ’چیز‘، گرفته شده بود، و دلیلش هم این بود که درست مانند ریاضیدانان
امروزی که از علامت x استفاده میکنند،
آنها نیز برای نشان دادن یک کمیت مجهول از یک علامت استفاده میکردند، و آن را چیز
مینامیدند. کلیه محاسبهگرهای این دوره، خودشان روشهای ماهرانه را برای انجام
محاسبات اختراع کرده بودند و نهایت سعی خود را میکردند که این روشها را مخفی
نگاه دارند، تا اعتبار حل فلان مسئله به خود آنها داده شود و نه کس دیگری. در این
میان نیکولو تارتاگیلا (Niccolò Tartaglia)
یک مورد استثنا بود. او روش سریعی برای حل معادلات درجه سوم یافته بود، و این کشف
را برای جرولامو کاردانو (Girolamo
Cardano) فاش کرده و او را قسم داده بود که هیچوقت این راز را
فاش نکند. ده سال بعد کاردانو کتابی بنام هنر والا (Ars Magna) نوشت و این روش را در آن فاش
کرد، عملی که تارتاگیلا هرگز آن را فراموش نکرد. او کلیه ارتباطات خودش با کاردانو
را قطع کرد و دشمنی تلخی بین آنان پدید آمد، و همین باعث شد تا بقیه ریاضیدانان از
اسرارشان بیشتر مواظبت کنند. طبیعت پنهانکارِ ریاضیدانان تا اواخر قرن نوزدهم
ادامه یافت، و همانطور که بعداً خواهیم دید، حتی در قرن بیستم نیز نوابغی بودند که
پنهانی بر روی مسائل ریاضی کار میکردند.
هنگامی که
پدر مرسن به پاریس آمد او مصمم بود تا درمقابل این سُنت نهانکاری بایستد و تلاش
کرد ریاضیدانان را ترغیب کند تا ایدههای خودشان را با هم رد و بدل کنند. این کشیش
بطور مرتب ملاقاتهایی را ترتیب میداد و بعدها گروه او، حلقه اصلی آکادامی فرانسه
را تشکیل دادند. هر موقع کسی از شرکت در جلسات سرباز میزد، مرسن هر چه از آن شخص
داشت، حتی نامههای محرمانه او را نیز برای گروه فاش میکرد. برای یک کشیش چنین
رفتاری اخلاقی نبود، ولی او این رفتار را بر این اساس توجیه میکرد که تبادل دانشِ
ریاضی هم برای ریاضیات و هم برای بشریت مفید است. این بیملاحظگیها باعث شد تا
رابطه میان مرسن و دکارت، که از بچگی با او همکلاس بود، خراب شود. مرسن نوشتههای
فلسفی دکارت، که مایه رنجش کلیسا بودند، را افشا کرد، ولی او به اعتبار خودش از
افکار دکارت دفاع میکرد، همان کاری که قبلاً در مورد گالیله انجام داده بود. در
دورانی که مذهب و جادو حکمفرما بود، مرسن از خِرد منطقی دفاع میکرد.
مرسن به
سراسر فرانسه سفر میکرد و خبر آخرین اکتشافات صورت گرفته را پخش میکرد. در یکی
از این سفرها او به سراغ فرما رفت، و حقیقتاً بنظر میرسد تنها کسی که فرما بطور
مرتب از طریق او با بقیه ریاضیدانان تماس داشته مرسن بوده است. تاثیری که مرسن بر
روی فرما داشت را فقط میتوان با تاثیر کتاب Arithmetica بر فرما مقایسه کرد. این کتابی بود که توسط دیوفانتوس، ریاضیدان یونان باستان،
در مورد علم حساب نوشته شده بود و همدم همیشگی فرما بود. حتی هنگامی که مرسن قادر
به سفر کردن نبود، او ارتباطش را با فرما و دیگران از طریق نامهنگاری حفظ میکرد.
پس از مرگ مرسن، در اطاق او نامههای زیادی پیدا شد که نشان میداد با هفتاد و هشت
نفر مکاتبه داشته.
عليرغم
تشویقهای مرسن، فرما بطور استواری از افشای اثباتهای خود سرباز میزد. برای فرما
انتشار آثارش یا مشهور شدن معنای نداشت و تنها دلخوشی او خلق قضایای جدید بود. ولی
این قاضی خجالتی یک رگ بدجنسی هم داشت، که با طبع نهانکار او ترکیب میشد. در چنین
مواقعی اگر فرما با ریاضیدانان دیگری ارتباط برقرار میکرد، اینکار را تنها برای
سر به سر گذاشتن آنها میکرد. او معمولاً نامههایی را به آنها مینوشت و در آن
آخرین قضایای خودش را بدون اینکه اثباتی برای آنها ارائه کند بیان میداشت. سپس او
همعصران خودش را بچالش میگرفت تا برای قضایای مطرح شده اثباتی را ارائه دهند.
اینکه او هیچگاه استدلالهای خودش را افشاء نمیکرد موجب استیصال بقیه بود. فیلسوف
و ریاضیدان فرانسوی رنه دکارت (Rene
Descartes) فرما را ’لاف زن‘ مینامید، و ریاضیدان انگلیسی جان
والیس (John Wallis) از او بعنوان
’فرانسوی لعنتی‘ یاد میکرد.
فرما
علاوه براینکه برای همکارانش مسائلی را طرح میکرد، آنهم بدون اینکه اثباتی برای
آنها ارائه دهد، و از اینکار لذت میبرد، ولی او انگیزههای عملی دیگری نیز برای
رفتار خودش داشت. اول این بود که او مجبور نبود بطور کامل روشهای خودش را پرورش
دهد، در عوض او میتوانست سریعاً به سراغ قضیه بعدی خود برود. بعلاوه او مجبور
نبود از خردهگیری حسادتمندانه دیگران رنج ببرد. اگر کسی چیزی را اثبات میکرد،
این اثبات بارها از طرف دیگران مرور میشد و مورد بحث قرار میگرفت. هنگامی که بلز
پاسکال (Blaise Pascal) به او فشار آورد تا
برخی از آثار خودش را منتشر کند، مرد منزوی در جواب گفت ”چه کارهای من ارزش انتشار
داشته باشند چه نه، نمیخواهم نام من آشکار شود“. فرما نابغه مرموزی بود که شهرتش
را فدای این کرد که از طرف منتقدینش مورد سئوال قرار نگیرد.
به غیر از مکاتباتی که فرما با مرسن داشت، تبادل
نامه با پاسکال تنها موردی بود که فرما با ریاضیدان دیگری مکاتبه میکرد. در آن
زمان پاسکال شاخه جدیدی از ریاضیات را خلق کرده بود که حالا نظریه احتمالات
(probability theory ) نامیده میشود. فرما
توسط پاسکال با این موضوع آشنا شده بود، و علیرغم میلش به انزوا، او خود را مجبور
میدید که با پاسکال گفتگویی را برقرار کند. پاسکال و فرما با هم اولین اثباتهای
محکم در نظریه احتمالات را ارائه دادند. کسی که باعث شد پاسکال به نظریه احتمالات
علاقهمند شود قمارباز معروف پاریسی آنتوان گومبو (Antoine Gombaud) بود، که یک بازی شانسی بنام امتیازات
(points) را مطرح کرده بود. بازی به
این صورت بود که بازیکنان باید با پرتاب طاس امتیازاتی را کسب میکردند، و بازیکنی
که اول از همه امتیازات معینی را کسب میکرد برنده بود و جایزه نقدی را میبرد.

بلز پاسکال (Blaise
Pascal) 1662-1623.
هنگامی که
گومبو با قمارباز دیگری مشغول بازی بودند، در میانه کار به آنها گفته شد که بازی
را متوقف کنند. مشکل این بود که در اینجا تکلیف پول جایزه چطور میشود. سادهترین
راه حل این بود که تمام جایزه به کسی داده شود که بیشترین امتیازات را کسب کرده
بود، ولی گومبو از پاسکال پرسید که آیا روش عادلانهتری برای تقسیم پول وجود دارد
یا نه. از پاسکال خواسته شد تا اگر هر یک از طرفین بازی را ادامه دهد، و شانس
برنده شدن هر دو آنها نیز برابر باشد، احتمال برنده شدن هر یک را حساب کند. بر این
اساس متناسب با احتمال برنده شدن هر یک آنها، میشد پول جایزه را میانشان تقسیم
کرد.
پیش از
قرن هفدهم قوانین احتمالات بر اساس ادراک و تجربه قماربازان معین میشد، ولی
پاسکال و فرما درگیر مکاتباتی شدند تا شاید بتوانند قواعد ریاضی را کشف کنند که
بتواند بطور دقیقتری قوانین شانس را توصیف کند. سه قرن بعد برتراند
راسل (Bertrand Russell) درمورد این عبارت
بظاهر ضد و نقیض اینطور اظهار نظر میکند: ”چگونه ما جرات میکنیم از قوانین شانس
صحبت کنیم؟ آیا شانس نقطه مقابل همه قوانین نیست؟“
این دو
ریاضیدان فرانسوی مسئله گومبو را تحلیل کردند و خیلی زود متوجه شدند این مسئله
سادهای است که میتوان با تعریف همه نتایج بالقوهِ بازی و تعیین یک احتمال برای
هر یک از آنها، آن را حل کرد. هم پاسکال و هم فرما قادر بودند به تنهای این مسئله
را حل کنند، ولی همکاری آنها موجب تسریع در حل این مسئله شد و آنها را به درک
عمیقتر سئوالات پیچیدهتری رهنمون کرد که با احتمالات رابطه داشتند.
برخی
اوقات مسائلی که با احتمالات سروکار دارند جنجالبرانگیز هستند، زیرا جوابهای
ریاضی، یا بعبارتی همان جوابهای قاطع و درست، غالباً با آنچه بصیرت انسان حکم میکند
در تضاد هستند. شاید این درماندگی بصیرت تعجب برانگیز باشد. یکی از مثالهای
مربوط به احتمالات، که برخلاف شهود ماست، مسئله احتمال یکسان بودن روز تولد بازیکنان
دو تیم فوتبال است.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
اندرو
وایلز با صدایی مردد که نشان دهنده هیجانی بود که نسبت به این مسئله داشت، برای من
اینطور تعریف کرد ”وقتی بچه بودم با آخرین قضیه فرما آشنا شدم، و از آن پس این
قضیه به بزرگترین علاقه من تبدیل شد. من مسئلهای را پیدا کرده بودم که برای بیش
از سیصد سال لاینحل مانده بود. بسیاری از همکلاسیهایم علاقه زیادی به ریاضیات
نداشتند، و به همین دلیل من هم این مسئله را با آنها در میان نگذاشتم. ولی در آن
زمان معلمی داشتیم که تحقیقاتی در ریاضیات کرده بود و به من کتابی داد که درباره
نظریه اعداد بود. با خواندن این کتاب نشانههایی را بدست آوردم که به من نشان داد
کارم را باید از کجا آغاز کنم. در آغاز من فرض را بر این گذاشتم که فرما به اندازهای
که من حالا ریاضیات بلدم، او بلد نبود. من سعی کردم راه حل گم شده او را با
استفاده از روشهایی پیدا کنم که ممکن بود او آنها را بکار برده باشد.“
در جایی
که نسلهای متمادی از ریاضیدانان ناکام مانده بودند، وایلز یک بچه کاملاً ساده و
جاهطلب بود که فرصتی برای موفقیت دیده بود. برای دیگران این یک رویای بیپروا
بنظر میرسید، ولی از یک نظر حق با وایلز جوان بود که پیش خودش فکر میکرد که او،
یعنی یک بچه مدرسهای قرن بیستمی، بیشتر ریاضیات بلد است تا پییر دو فرما، یعنی
یک نابغه ریاضی قرن هفدهمی. از نگاه ساده وایلز، شاید او میتوانست اثباتی را پیدا
کند که از دید ریاضیدانان دیگر پنهان مانده باشد.
علیرغم
شوقی که داشت، در آخر تمام محاسبات او به بنبست برخورد کردند. هرچه به مغز خودش
فشار آورد و کتابهای درسی خودش را زیر رو کرد، هیچ چیزی عایدش نشد. پس از یک سال
شکست او استراتژی خودش را تغییر داد و تصمیم گرفت که ممکن است بتواند از اشتباهات
ریاضیدانان برجسته درس بگیرد. او گفت ”آخرین قضیه فرما یک تاریخ عاشقانه را به همراه
خودش دارد. افراد بسیاری درباره آن فکر کردهاند، و هر چه ریاضیدانان بزرگ در
گذشته برای حل آن تلاش کردن و در این راه شکست خوردند، این قضیه نیز به چالشی
بزرگتر و معمای عجیبتری بدل شد. در قرنهای هجدهم و نوزدهم بسیاری از ریاضیدانان
سعی کردند از راههای مختلفی این مسئله را حل کنند، و من هم بعنوان یک نوجوان
تصمیم گرفتم که باید این روشها را مطالعه کنم و سعی کنم بفهمم که آنها چه
اشتباهاتی را مرتکب شدهاند.“
وایلز جوان همه رویکردهایی را که دیگران در مواجهه
با آخرین قضیه فرما اخذ کرده بودند را مطالعه کرد. او کار خودش را با مطالعه
آثار پرکارترین ریاضیدان تاریخ آغاز کرد، کسی که برای اولین بار توانسته بود در
مبارزه با فرما پیروزیهایی را بدست آورد.
آفرینش
ریاضی کاری پرزحمت و اسرارآمیز است. غالباً هدف از اثباتِ ریاضی روشن است، ولی
مسیر آن در مه قرار دارد. ریاضیدانانی که درگیر محاسبهای میشوند، از این هراس
دارند که هر قدمی که برمیدارند باعث شود استدلال آنها به جهت کاملاً اشتباهی
هدایت شود. همچنین این هراس نیز وجود دارد که اصلاً راهی برای اثبات وجود نداشته
باشد. یک ریاضیدان ممکن است عقیده داشته باشد که یک عبارت صحیح است، و سالها وقت
خود را بر روی اثباتِ صحیح بودن آن بگذارد، در حالی که در واقع این عبارت نادرست
بوده. در اصل کاری که ریاضیدان انجام میداده، سعی در اثبات یک چیز محال بوده.
در تمام
تاریخ این رشته، تنها ریاضیدانان معدودی بودهاند که توانستهاند از عدم اعتماد
بنفسی که موجب هراس همکاران آنها بودهاند دوری کنند. شاید مهمترین مثال چنین
ریاضیدانانی لئونارد اویلر باشد، که یک نابغه سوئیسی قرن هجدهم، و اولین
کسی بود که در اثبات آخرین قضیه فرما قدمهای مهمی را برداشت. گفته میشد که اویلر
چنان بصیرت بالا و حافظه قوی داشت که قادر بود کُل یک محاسبه پیچیده را در ذهن
خودش انجام دهد، آنهم بدون اینکه نیاز به قلم و کاغذ داشته باشد. اویلر بواسطه
تسلطی که بر آنالیز ریاضی داشت، در سراسر اروپا به ’آنالیز مجسم‘ معروف بود، و
دانشمند فرانسوی، فرانسوا آراگو (François Arago)
در باره او میگفت ”اویلر به همان سادگی که انسان نفس میکشد، یا عقاب خودش را در
هوا نگاه میدارد، محاسبات را انجام میدهد.“
لئونارد
اویلر (Leonhard Euler) در سال 1707 در شهر بازل
بدنیا آمد. پدرش کشیشی بنام پُل اویلر بود. هرچند اویلر در کودکی نبوغ ریاضی
فراوانی از خودش نشان داده بود، ولی پدرش مصمم بود که او باید الهیات بخواند و
نهایتاً منصبی را در کلیسا پیدا کند. اویلر از خواسته پدر پیروی کرد و در دانشگاه
بازل به مطالعه الهیات و زبان عبری پرداخت.
شهر بازل موطن خاندان برنولی (Bernoulli) نیز بود. براحتی میتواد ادعا
کرد که برنولیها معروفترین خانواده ریاضیدان بودند، که طی سه نسل هشت تن از
برجستهترین ریاضیدانان اروپا را تربیت کردند. برخی میگویند که خاندان برنولی
برای ریاضیات همان وضعیتی را داشت که خاندان باخ برای موسیقی. شهرت آنها از جامعه
ریاضی فراتر رفته بود و یکی از آنها، یعنی دانیل برنولی (Daniel Bernoulli) نمونه مشخص این خانواده بود.
روزی دانیل که مشغول سفر در اروپا بود با غریبهای آشنا شد. پس از مدتی او با
فروتنی خودش را معرفی کرد و گفت: ”من دانیل برنولی هستم“. مرد غریبه نیز بطور
کنایه آمیزی گفت ”من هم آیزاک نیوتون هستم“. دانیل که چندین بار با چنین وضعیتی
روبرو شده بود، چنین برخوردهایی را نشانهای از حسن شهرت خودش میدید.

لئونارد اویلر (Leonhard
Euler) 1783-1707
دانیل و
نیکولاس برنولی از دوستان نزدیک لئونارد اویلر بودند، و آنها میدیدند که
بااستعدادترین ریاضیدان جهان دارد به یک روحانی بد تبدیل میشود. آنها نزد پُل
اویلر، پدر لئونارد، رفتند و ملتمسانه از او تقاضا کردند که به لئونارد اجازه داده
شود تا لباس روحانیت را از تن درآورده و به مطالعه ریاضیات بپردازد. پل که خودش در
گذشته نزد برنولی بزرگ، یعنی ژاکوب برنولی، ریاضیات خوانده بود
احترام زیادی برای این خانواده قائل بود. نهایتاً او با بیمیلی پذیرفت که پسرش
برای محاسبه زاده شده نه برای موعظه.
بزودی
لئونارد اویلر سوئیس را ترک کرد و به شهرهایی مثل برلین و سنت پیترزبورگ رفت،
جاهایی که خلاقانهترین سالهای زندگی خودش را در آنجا سپری کرد. در زمان فرما
ریاضیدانان را افراد آماتوری میدانستند که کارشان تردستی با اعداد است، ولی در
قرن هیجدهم آنها را به عنوان افراد حرفهای مسئله-حل کن بحساب میآوردند. فرهنگ
ریاضی کلاً دگرگون شده بود، و بخشی از آن بخاطر محاسبات علمی سر آیزاک
نیوتون (Sir Isaac Newton)
بود.
نیوتون عقیده داشت که ریاضیدانان با طرح معماهای
بیهوده برای یکدیگر دارند وقت خودشان را تلف میکنند. در عوض او ریاضیات را برای
جهان فیزیکی بکار گرفت و همه چیز را از مدار سیارات تا مسیر پرتاب گلوله توپ
محاسبه کرد. تا سال 1727 که نیوتون فوت کرد، اروپا دستخوش یک انقلاب علمی شده بود،
و در همان سال بود که اویلر اولین مقاله خودش را منتشر کرد. هرچند این مقاله شامل
ریاضیات نوآورانه و زیبایی بود، ولی هدف اصلی آن حل یک مسئله فنی مربوط به دکل
کشتیها بود.

آیزاک نیوتون (Isaac
Newton) 1727-1642
قدرتهای
اروپایی علاقهای به حل مسائل عجیب و مفاهیم انتزاعی ریاضی نداشتند؛ در عوض آنها
میخواستند از ریاضیات برای حل مسائل عملی استفاده کنند، و برای بکارگیری
بهترین مغزهای اروپا با یکدیگر رقابت میکردند. اویلر پیش از اینکه به دعوت فردریک
کبیر به آکادمی برلین برود، کار خودش را با تزارهای روسیه شروع کرد. سرانجام او به
روسیه تحت فرامانروایی کاترین کبیر بازگشت، و سالهای واپسین عمر خودش را در آنجا
سپری کرد. او در طول عمرش مسائل بسیاری، از مسائل مربوط به دریانوردی گرفته، تا
امور مالی، آکوستیک، و آبیاری را حل کرد. طبیعتِ کاربردی این مسائل تاثیری بر
تواناییهای ریاضی اویلر نداشت. در عوض، او با هر مشکل جدیدی که روبرو میشد، این
برایش الهام بخش ساخت یک ریاضیاتِ مبتکرانه و نوآورانه میشد. اویلر اشتیاق و
پشتکار فراوانی داشت، و این باعث میشد که تنها در یک روز چندین مقاله بنویسد، و
گفته میشد از زمانی که برای ناهار او را صدا میکردند تا زمانی که بر سر میز حاضر
میشد میتوانست محاسبات کاملی را انجام دهد که ارزش چاپ کردن داشت. او یک لحظه را
هم تلف نمیکرد. حتی هنگامی که با یک دست کودک خردسالش را در گهواره تکان میداد،
با دست دیگرش مشغول طرح ریزی اثبات یک قضیه بود.
یکی از
بزرگترین دستآوردهای اویلر توسعه روشهای الگوریتمی بود. هدف الگوریتمهای اویلر
رسیدگی به مسائلی بود که ظاهراً ناممکن بودند. یکی از این مسائل پیشبینی حالتهای
ماه با دقت بالا، و در آیندههای دور بود- اطلاعاتی که با استفاده از آن میشد
جداول دریانوردی حیاتی را رسم کرد. نیوتون قبلاً نشان داده بود که به آسانی میتوان
مدار جسمی که به دور جسم دیگری درحال چرخش است را حساب کرد، ولی در مورد ماه وضعیت
آنقدرها ساده نیست. ماه بدور زمین میگردد، ولی جسم سومی نیز هست و آن خورشید است
که موضوع را خیلی پیچیدهتر میکند. در همان حالی که زمین و ماه یکدیگر را جذب میکنند،
خورشید موقعیت زمین را آشفته میکند و این بر روی مدار ماه یک تاثیر ثانویه میگذارد.
میتوان از معادلات برای مشخص کردن تاثیراتی که دو جسم بر روی یکدیگر میگذارند
استفاده کرد، ولی ریاضیدانان قرن هجدهم قادر نبودند تا جسم سومی را به محاسبات
خودشان وارد کنند. حتی امروزه هم غیرممکن است که بتوان جواب این مسئله را، که به
’مسئله سه-جسم‘ (three-body problem)
معروف است، دقیقاً پیشبینی کرد.
اویلر
متوجه شده بود که دریانوردان نیازی ندارند تا بطور کاملاً دقیق حالتهای ماه را
بدانند، بلکه آنها تنها به آن اندازه از دقت نیاز دارند که بتوانند با اختلاف چند
میل دریایی موقعیت خودشان را در دریا مشخص کنند. درنتیجه اویلر برای تولید یک جواب
ناقص دستور العملی را ارائه داد. هرچند جواب حاصله ناقص بود، ولی بهاندازه کافی
دقیق بود. این دستورالعمل، که الگوریتم (algorithm)
نامیده میشود، ابتدا یک جواب آزمایشی تولید میکند، که میتوان آن را دوباره به
خورد الگوریتم داد تا جواب دقیقتری را تولید کند. سپس این جواب بهبودیافته را میتوان
دوباره به الگوریتم بازخوراند تا باز هم جوابی را تولید کند که نسبت به قبلی
دقیقتر است، و به همین ترتیب این را ادامه داد. با تکراری درحدود صد بار، اویلر میتوانست
موقعیت ماه را طوری مشخص کند که برای امور دریانوردی کافی بود. او الگوریتم خودش
را در اختیار نیروی دریایی بریتانیا قرار داد و آنها نیز در بازگشت از سفر به او
300 پوند جایزه دادند.
اویلر به
این معروف شده بود که میتواند هر مسئلهای را که درمقابل او قرار میدهند حل کند،
استعدادی که بنظر میرسید حتی خارج از قلمرو علوم نیز گسترش دارد. در طول دوران
خدمتش در دربار کاترین کبیر، اویلر با فیلسوف بزرگ فرانسوی دنیس دیدرو
(Denis Diderot) روبرو شد. دیدرو
فیلسوفی بود که به خدا اعتقادی نداشت و هنگامی که در روسیه بسر میبرد مردم را به
خدانشناسی ترغیب میکرد. کاترین که از این موضوع بسیار خشمگین بود از اویلر خواست
که به تلاشهای این فرانسوی خدانشناس پایان دهد. اویلر کمی درمورد این مسئله فکر
کرد و ادعا کرد که او برای اثبات وجود خدا یک اثبات جبری دارد. کاترین کبیر اویلر
و دیدرو را به کاخ خودش دعوت کرد و درباریان را نیز فراخواند تا به این بحث مذهبی
گوش دهند. اویلر رو به حضار کرد و گفت:
”ببینید آقا، ![]() ، پس خدا وجود دارد، پاسخ دهید!“
، پس خدا وجود دارد، پاسخ دهید!“
دیدرو که معلومات جبری چندانی نداشت و قادر نبود با
بزرگترین ریاضیدان اروپا بحث کند، بدون اینکه قادر به صحبت باشد تالار را ترک کرد.
او که تحقیر شده بود سنت پیترزبورگ را ترک کرد و به پاریس بازگشت. در غیاب او
اویلر از بازگشت به الهیات خوشنود بود و چندین کتاب را منتشر کرد که در آنها اثباتهای
ساختگی در رابطه با خدا و روح انسان را ارائه داده بود.
شکل 5. رودخانه پریگل، شهر کونیگزبرگ را به
قسمتهای A، B،
C، و D
تقسیم میکند. هفت پل قسمتهای مختلف شهر را به یکدیگر وصل میکند. یک معما هست که
میگوید آیا امکان دارد بدون اینکه بیشتر از یکبار از هر یک پلها عبور کرد، به کل
قسمتهای شهر سفر کرد؟
مسئله معتبرتری که به نظر وسواسی اویلر جالب آمده
بود چیزی بود که به پلهای شهر کونیگزبرگ (Königsberg)
مربوط بود، که حالا شهر کالنینگراد (Kaliningrad)
نامیده میشود و در روسیه فعلی قرار دارد. این شهر در کنار ساحل رودخانه پریگل
ساخته شده است و شامل چهار قسمت است که توسط هفت پُل به یکدیگر متصل شدهاند. نمای
کلی شهر در شکل 5 دیده میشود. برخی از ساکنان کونیگزبرگ که کنجکاوتر بودند میخواستند
بدانند که آیا امکان دارد به کل قسمتهای شهر سفر کرد بدون اینکه لازم باشد بیشتر
از یکبار از هر هفت پل عبور کرد؟ ساکنان کونیگزبرگ مسیرهای گوناگونی را امتحان
کرده بودند که همه آنها به شکست انجامیده بود. اویلر نیز نتوانسته بود مسیر درستی
را پیدا، ولی او توانست توضیح دهد که چرا چنین مسیری ممکن نیست.
شکل 6. نمای سادهای از پُلهای کونیگزبرگ.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
بدنبال
کارهای ارنست کومر، امید برای پیدا کردن اثباتی برای آخرین قضیه فرما کمرنگتر از
همیشه بنظر میرسید. بعلاوه ریاضیدانان شروع کرده بودند به حوزههای مطالعاتی متفاوتی
قدم بردارند، و این خطر وجود داشت که نسل جدید ریاضیدانان، قضیه فرما را بعنوان یک
مسئله غیرممکن و بینتیجه در نظر بگیرند. این مسئله هنوز هم تا ابتدای قرن بیستم
جایگاه بخصوصی در قلب متخصصین اعداد داشت، ولی نظر آنها درمورد آخرین قضیه فرما
مانند نظر شیمیدانان درمورد کیمیاگری بود. شباهت آنها در این بود که هر دو
رویاهای احمقانهای بودند که به گذشته تعلق داشتند. سپس یک سرمایهدار آلمانی بنام
پُل ولفسکِل (Paul Wolfskehl)
وارد صحنه شد و جان تازهای به این مسئله بخشید. خانواده ولفسکل بخاطر ثروت و
پشتیبانی خودشان از هنر و علم معروف بودند، و در این میان پل هم استثنا نبود. او
در دانشگاه ریاضی خواند بود و گرچه بیشتر زندگی خودش را به توسعه شغل خانوادگی
خودش اختصاص داد، ولی ارتباطش را با ریاضیدانان حرفهای حفظ کرد و بطور تفریحی بر
روی نظریه اعداد کار میکرد. خصوصاً ولفسکل در مقابل آخرین قضیه فرما تسلیم نشد.
ولفسکل از
هیچ نظر ریاضیدان بااستعدادی نبود و تقدیر هم نبود که او در پیدا کردن اثباتی برای
آخرین قضیه فرما سهم عمدهای داشته باشد. بااینحال، به لطف یک سری پیشآمدهای
عجیب، نام او تا ابد با مسئله فرما گره خورد، و مایه الهام هزاران ریاضیدان شد تا
این چالش را ادامه دهند.
داستان از
اینجا شروع شد که ولفسکل عاشق زن زیبایی شده بود که هویت او هرگز محرز نشد. از
بختِ بدِ ولفسکل، این زن مرموز دست رد بر سینه او زد و او چنان احساس بیچارگی کرد
که تصمیم به خودکشی گرفت. او مرد پرشوری بود، ولی خیلی هم عجول نبود، و به همین
دلیل تصمیم گرفت جزئیات خودکشی خودش را بطور دقیق برنامه ریزی کند. او تاریخی را
برای اینکار تعیین کرد و قصد داشت با شلیک به سرش، دقیقاً در نیمه شب خودکشی کند.
در روزهای باقیمانده او به کلیه امورِ مهمِ تجاری خودش رسیدگی کرد، و قرار بود
وصیتنامه خودش را در آخرین روز بنویسد و برای تمام دوستان نزدیک و خانوادهاش نامه
خداحافظی بفرستد.
ولفسکل
همه کارهای مقرر خودش را انجام داد، ولی آنها را زودتر از نیمه شب بپایان رساند،
سپس برای اینکه چند ساعتِ باقیمانده را تلف کند، به کتابخانه رفت و شروع به گشتن
در میان کتابهای ریاضی کرد. زیاد طول نکشید که به مقاله کلاسیک کومر برخورد کرد که
دلیل ناکامی کوشی و لامه را توضیح میداد. این یکی از بهترین مقالههای ریاضی آن
زمان بود و برای سپری کردن آخرین لحظات مرگ یک ریاضیدانِ درحالِ خودکشی، چه چیزی
میتوانست بهتر از خواندن این مقاله باشد. ولفسکل محاسبات کومر را خط به خط دنبال
کرد. ولی ناگهان به موردی برخورد که بنظر میرسید اشکالی در استدلال باشد و همانجا
در جای خودش میخکوب شد، کومر چیزی را فرض گرفته بود و در استدلال خودش فراموش کرده
بود آن را توجیه کند. ولفسکل نمیدانست که آیا او توانسته در استدلال کومر یک نقص
جدی را پیدا کند یا اینکه فرض او واقعاً موجه بوده. اگر مورد اول درست بود، آنگاه
احتمال داشت که اثبات نظریه فرما سادهتر از آن باشد که قبلاً تصور میشد.
او نشست و
قسمت ناقص استدلال را بررسی کرد، و به این فکر فرو رفت که اثباتی را ارائه دهد که
یا شکاف استدلال کومر را پر کند یا ثابت کند که فرض وی اشتباه بوده، که در
اینصورت کار کومر بیاعتبار میشد. کار او تا صبح ادامه داشت، شکاف اثبات کومر هم
پر شده بود، ولی آخرین قضیه فرما هنوز هم در حوزه دستنیافتنیها باقی مانده بود و
تا آنجا که به خود ریاضیات مربوط بود، این خبر بدی بود. ولی خبر خوب این بود که از
موعد مقرر برای خودکشی گذشته بود، و ولفسکل از اینکه توانسته بود شکافی را در کارِ
کومرِ بزرگ پیدا کند چنان بر خودش بالید که غم و نامیدی او برطرف گشت. ریاضیات
باعث شده بود تا او به زندگی امیدوار شود.
ولفسکل
نامههای خداحافظی خودش را پاره کرد و بر اساس آنچه آنشب اتفاق افتاده بود وصیت
نامه جدیدی را تنظیم کرد. بمحض فوت او در سال 1908 وصیتنامه جدید او خوانده شد. پل
مقدار زیادی از ثروتش را وقف جایزهای کرده بود که باید به کسی داده شود که بتواند
آخرین قضیه فرما را اثبات کند، که این باعث شگفتی خانواده او شد. مبلغ این جایزه
یک صدهزار مارک آلمان بود که به پول حالا چیزی حدود یکمیلیون و پانصدهزار دلار میشود.
او این جایزه را به شکرانه معمایی میداد که زندگی او را نجات داده بود.
این پول
در اختیار یک هیئت علمی قرار گرفت که همان سال شروع رقابت برای جایزه ولفسکل را
اعلام کرد:
طبق
اختیاراتی که از طرف مرحوم دکتر پل ولفسکل به ما داده شده، اعلام میکنیم که مبلغ
یکصد هزار مارک به شخصی داده میشود که بتواند اول از همه قضیه فرما را اثبات کند.
و سپس این
هیئت در ادامه اعلامیه شرایط و قواعد مسابقه را اعلام کرد.
جالب است
که طبق شرایط مسابقه، یک صد هزار مارک به اولین ریاضیدانی داده میشد که ثابت میکرد
آخرین قضیه فرما صحیح است، ولی اگر کسی پیدا میشد و ثابت میکرد این قضیه غلط
است، به او حتی یک سکه هم داده نمیشد.
جایزه
ولفسکل در کلیه نشریات ریاضی اعلام شد و خبر این رقابت در سراسر اروپا پیچید. علیرغم
تلاش تبلیغاتی و مشوق بزرگی که جایزه ولفسکل بهمراه داشت، این باعث نشد تا توجه
تعداد زیادی از ریاضیدانان بزرگ به این مسئله جلب شود. اکثر ریاضیدانان حرفهای به
آخرین قضیه فرما بعنوان یک هدف شکست خورده نگاه میکردند و تصمیم گرفته بودند تا
وقت و توان خودشان را با کار بر روی یک ماموریت احمقانه تلف نکنند. ولی این جایزه
موفق شد توجه مخاطبین جدیدی را به مسئله جلب کند، تعداد زیادی از افراد بااستعداد که
حاضر بودند خودشان را فقف این معمای غایی کنند.
از زمان
یونانیان تا کنون، ریاضیدانان بدنبال این بودهاند تا با بیان اثباتها و قضیههای
خودشان بشکل جداول عددی، رنگ و بوی جالبتری به آنها بدهند. این رویکرد بامزه در طول
نیمه دوم قرن نوزدهم راه خوش را به نشریات عامهپسند باز کرد و جداول عددی را میشد
در کنار جداول کلمات پیدا کرد. از طرف دیگر آماتورها بر روی هر مسئلهای کار میکردند،
از معماهای پیش و پا افتاده گرفته تا مسائل مشکل ریاضی، و از جمله آخرین قضیه
فرما، به همین دلیل هم مخاطبین معماهای ریاضی در حال زیادتر شدن بود.
شاید
بتوان گفت که پرکارترین سازنده چنین معماهایی هنری دودنی (Henry Dudeney) بود، که برای بسیاری از
مجلات، از جمله Strand, Cassell’s , the Queen, Tit-Bits, the Weekly Dispatch و
Blighty، کار میکرد. از دیگر کسانی
که در دوران ویکتوریا به کار ساختن جداول مشغول بودند میتوان به کشیش چارلز
داجسون (Charles Dodgson)
اشاره کرد که در آکسفورد مدرس ریاضی بود، و بیشتر با نام مستعار لوئیس کارول
(Lewis Carroll) شناخته میشود.
داجسون چندین سال وقت خودش را صرف گردآوری مجموعه بزرگی از معماهای ریاضی کرد و
آنها را تحت نام Curiosa Mathematica
منتشر کرد. هر چند این سری ناتمام مانده بود ولی چند جلد دیگر از جمله Pillow Problems را نیز منتشر کرد.
بزرگترین
معماساز آن زمان یک نابغه آمریکایی بنام سَم لوید (Sam Loyd [1841–1911]) بود، که توانست در
دوران نوجوانی با ساختن جداول جدید و تغییر جداول قدیمی برای خودش ثروتی خوبی را
دست و پا کند.
مشهورترین
ساخته لوید، که معادل مکعب روبیک قرن بیستم بود، جدولی است که ’14-15‘ نامیده میشود، و
هنوز هم میتوان در برخی فروشگاهها آن را پیدا کرد[2].
در این معما پانزده کاشی قرار دارند که هر کدام از 1 تا 15 شمارهگذاری شدهاند و همه
آنها در یک جدول 4×4
قرار گرفتهاند. هدف از این بازی این است که با لغزاندن کاشیها به اطراف، بتوان آنها
را بطور مرتب چید. لوید مبلغ قابلملاحظهای (1000 دلار آن زمان) برای کسی جایزه
گذاشت که بتواند با یک سری از حرکات جای کاشیهای ’14‘ و ’15‘ را در مکان درست خودشان قرار
دهد.
لوید همیشه مطمئن بود که او مجبور نخواهد بود این
1000 دلار را به کسی بدهد، زیرا میدانست که غیر ممکن است که بدون اینکه نظم کاشیهای
دیگر جدول را بهم زد بتوان جای دو کاشی را با هم عوض کرد. به همان طریقی که یک
ریاضیدان میتواند ثابت کند یک معادله هیچ جوابی ندارد، لوید هم توانست ثابت کند
که جدول ’14-15‘
غیرقابل حل است.
شکل
12. با لغزاندن کاشیها به
اطراف میتوان جدول را بصورتهای مختلفی نامرتب کرد. برای هر چیدمانی که انجام میشود،
میتوان میزان نامرتب بودن جدول را با استفاده از پارامتری بنام Dp نشان داد.
اثبات
لوید با تعریف کمیتی آغاز میشود که میزان نامرتب بودن یک جدول را مشخص میکند، و
آن را Dp مینامید. پارامتر بینظمی
برای هر چیدمان عبارت است از تعداد جفتهایی که ترتیب آنها اشتباه است. بنابراین
همانطور که در شکل 12(a)
نشان داده شده، چون در یک جدول صحیح هیچ جفتی نیست که ترتیب آن اشتباه باشد، پس Dp=0 است.
اگر کار
را با جدولی شروع کنیم که درست چیده شده و سپس کاشیها را به اطراف بلغزانیم، خیلی
ساده میتوان به چیدمانی رسید که در شکل 12(b) نشان داده شده. در اینحالت
کاشیها تا قبل از اینکه به کاشی 11 و 12 برسیم ترتیب درستی دارند. واضح است که کاشی 11 باید پیش از 12 بیاید، و بنابراین
ترتیب این این جفت اشتباه است. فهرست جفت کاشیهایی که ترتیب آنها اشتباه است
عبارتند از: (12,11),
(15,13), (15,14), (15,11), (13,11) و (14,11). حالا که ترتیب شش جفت اشتباه
است، بنابراین پارامتر بینظمی، Dp=6 خواهد بود. (توجه کنید که کاشیهای 10 و 12 پهلوی هم قرار دارند،
که اشتباه است، ولی ترتیب کوچک به بزرگ آنها درست است، بنابراین چنین حالتهایی در
محاسبه پارامتر بینظمی بحساب نمیآیند.)
بعد از
کمی جابجایی بیشتر ما چیدمانی را خواهیم داشت که در شکل 12(c) نشان داده شده. اگر شما
فهرستی از جفت کاشیهایی را بنویسید که ترتیب کوچک به بزرگ آنها درست نیست، خواهید
دید که Dp=12
است. نکتهای که باید به آن توجه کنید این است که در کلیه حالتهای(a)، (b) و (c)، مقدار پارامتر بینظمی یک عدد زوج است (0، 6، و 12). در واقع اگر شما
کارتان را با یک جدولِ مرتب آغاز کنید و به طریقی آن را دوباره بازچینی کنید، چنین
چیزی همیشه صادق است. تا وقتی مربع خالی نهایتاً در گوشه پایینی سمت راست قرار
بگیرد، هر طور هم که کاشیها جابجا شوند، نتیجه آن مقدار زوجی برای Dp خواهد بود. اینکه مقدار پارامتر بینظمی
یک عدد زوج است خاصیت جداییناپذیر هر چیدمانی است که از یک چیدمان اولیه صحیح
حاصل میشود. در ریاضیات آن خاصیتی که همیشه مقدار خود را حفظ میکند، آنهم
بدون توجه به اینکه چه بر سر شیء مورد نظر میآید، تغییرناپذیر
یا ناوردا (invariant)
نامیده میشود.
ولی اگر
شما چیدمانی که توسط لوید فروخته میشد، و در آن جای کاشیهای 14 و 15 با هم عوض شده بود را
در نظر بگیرید، آنگاه پارامتر بینظمی یک است (Dp=1)، و این یعنی تنها کاشیهایی که از ترتیب خارجاند جفت
(14
و 15)
هستند. بعبارتی دیگر، پارامتر بینظمی برای چیدمان لوید یک عدد فرد است! بااینحال
ما میدانیم که هرگونه چیدمانی که از چیدمان صحیح حاصل شود پارامتر بینظمی آن عدد
زوجی خواهد بود. نتیجه این است که از چیدمان صحیح نمیتوان به چیدمان لوید رسید، و
همینطور بالعکس، از چیدمان لوید هم نمیتواند به یک چیدمان صحیح و مرتب رسید، و
پول لوید همیشه محفوظ میماند!
معمای
لوید و پارامتر بینظمی نشان دهنده قدرت تغییرناپذیرها است. تغییرناپذیرها برای
ریاضیدانان راهبرد مهمی را فراهم میآورند تا اثبات کنند غیرممکن است بتوان شیئی
را به شیء دیگری تبدیل کرد. برای مثال، در حال حاظر حوزه هیجان انگیزی در ریاضیات
هست که به مطالعه گرهها (knots)
مربوط است، و بطور طبیعی برای نظریهپردازان گرهها جالب است تا اثبات کنند آیا میتوان
یک گره را تنها با پیچاندن و حلقه کردن، ولی بدون بریدن، به یک گره دیگر تبدیل
کرد. برای پاسخ به این سئوال آنها تلاش میکنند خاصیتی را در گره اولیه پیدا کنند
که هر چقد هم که پیچانده و یا حلقه شود آن خاصیت تغییر نکند، که این یک ناوردای
گره را تشکیل میدهد. آنگاه آنها همین خاصیت را برای گره دوم حساب میکنند. اگر
این دو مقدار با هم متفاوت بودند، آنگاه نتیجه این است که غیر ممکن است از گره اول
به گره دوم رسید.
تا وقتی
چنین تکنیکی در سالهای 1920 توسط کورت رِیدمیستر (Kurt Reidemeister) اختراع نشده بود، اثبات
اینکه یک گره را بتوان به گره دیگری تبدیل کرد غیر ممکن بود. به عبارت دیگر، تا
وقتی ناورداهای مربوط به گرهها کشف نشده بودند، غیره ممکن بود بتوان ثابت کرد که
یک گره چهار گوش اساساً با یک گره دو حلقهای، یا یک گره ماهیگیری، یا حتی یک حلقه
ساده که هیچ گرهای نخورده متفاوت هستند. مفهوم یک خاصیت ناوردا در بسیاری از
اثباتهای ریاضی دیگر هم نقش اساسی را دارد، و همانطور که در فصل 5 خواهیم دید، برای وارد کردن آخرین قضیه
فرما به ریاضیاتِ معاصر، استفاده از ناورداها حیاتی است.
به لطف سم
لوید و معمای ’14-15‘
او، در ابتدای قرن بیستم در سراسر اروپا و آمریکا میلیونها مسئله-حلکنِ آماتور
بودند که مشتاقانه بدنبال چالشهای جدیدی میگشتند. هنگامی که خبر جایزه ولفسکل به
گوش این ریاضیدانان جوان رسید، بار دیگر آخرین قضیه فرما به معروفترین مسئله جهان
تبدیل شد. در مقایسه با سختترین معماهای لوید هم، مطمئناً آخرین قضیه فرما از
آنها بسیار پیچیدهتر بود، ولی جایزه آن هم بسیار بیشتر بود. آماتورها خواب آن
روزی را میدیدند که شاید با استفاده از ترفندی که تا کنون بفکر هیچ استاد بزرگ
ریاضی نرسیده بتوانند راه حل سادهای برای این مسئله پیدا کنند. از نظر اطلاع از
تکنیکهای ریاضی، آماتورهای قرن-بیستمی با خود پییر دو فرما برابری میکردند. چالش
این بود که آیا آنها میتوانستند آن خلاقیتی را هم که فرما در تکنیکهایش بکار میبرد
داشته باشند.
چند هفته
از اعلام جایزه ولفسکل نگذشته بود که انبوهی از جوابها به دانشگاه گوتینگن سرازیر
شد. تعجببرانگیز نبود که تمام این اثباتها غلط بودند. هرچند هر یک از شرکت
کنندگان براین باور بودند که این مسئله چند-صد ساله را درست حل کرده بودند، ولی
همه آنها در استدلالات خودشان اشتباهات کوچک، و گاهی اوقات نه چندان کوچکی، را
مرتکب شده بودند. هنر نظریه اعداد چنان انتزاعی است که براحتی امکان آن هست که از
مسیر منطق خارج، و ناآگاهانه در گزافهگویی غرق شد. در ضمیمه 7 یک نمونه از خطاهایی نشان داده میشود که
ممکن است به آسانی از دید یک آماتور مشتاق پنهان بماند.
صرف نظر از
اینکه چه کسی اثبات را میفرستاد، تک تک آنها باید با دقت زیادی بررسی میشدند تا
هیچ اثبات معتبری، که ممکن بود از طرف یک آماتور ناشناس فرستاده شده، از نظر دور
نماند. رئیس بخش ریاضی دانشگاه گوتینگن بین سالهای 1909 تا 1934 پرفسور ادموند
لاندو (Edmund Landau) بود، و مسئولیت
بررسی جوابهای ارسالی برای جایزه ولفسکل را به عهده داشت. لاندو متوجه شد اثباتهای
درهم برهمی که ماهانه بطور بیوقفه روی میز او تلمبار میشوند موجب مختل شدن
تحقیقات او شده. این استاد ریاضی برای مقابله با وضعیت روشی را اختراع کرد که
کارها را جمع و جور کند. او صدها کارت را به صورت زیر چاپ کرد:

سپس لاندو
هر یک از این کارتها را به یکی از دانشجویان خودش میداد تا جاهای خالی را پر
کنند.
حتی بعد
از کاهش چشمگیر ارزش جایزه ولفسکل، که در اثر تورم شدیدی که پس از جنگ جهانی اول
پدید آمده بود، باز هم تا سالها از شدت ارسال این پاسخها کاسته نشد. شایعاتی هست
که میگوید اگر امروز کسی برنده جایزه بشود، با این پول حتی نمیتواند یک فنجان
قهوه هم برای خودش بخرد، ولی این ادعاها بیش از حد اغراقآمیز هستند. از دکتر اف.
شیلیکتیگ (F. Schlichting) ، که در دهه 1970 مسئول رسیدگی به پاسخها بود،
نامهای موجود است که در آن توضیح داده میشود که ارزش جایزه هنوز هم بیش از ده
هزار مارک آلمان است. این نامه که خطاب به ریاضیدان برزیلی پائلو ریبنبوئیم (Paulo Ribenboim) نوشته شده، و در کتاب او بنام 13 درس
درباره آخرین قضیه فرما به چاپ رسیده، وضعیت کمیتهای که مسئولیت جایزه ولفسکل
را برعهده داشت بخوبی روشن میکند:
آقای عزیز
از شمار
’جوابهایی‘ که تا کنون به این کمیته فرستاده شده هیچ اطلاعی در دست نیست. آن
تعدادی که در سال نخست (1908-1907) در دفتر ما ثبت شده 621 عدد بود، و حجم این
نامهها تا به امروز به بیش از 3 متر رسیده. در دهههای اخیر منشی آکادامی این
نامهها به طریق زیر دسته بندی میکرد:
(1)
مواردی که کاملاً مهمل بودند،
(2)
مواردی که بنظر حاوی ریاضیات
هستند.
دسته دوم
این نامهها به بخش ریاضیات دانشگاه فرستاده میشوند، که در آنجا کارِ خواندن،
پیدا کردن اشتباهات، و پاسخگویی به عهده یکی از دانشیاران گذاشته میشود، که در
حال حاضر قربانی این کار اینجانب است. در هر ماه باید به 3 یا 4 نامه پاسخ دهم، و
این شامل موارد عجیب و مضحک نیز میشود؛ مثلاً اینکه کسی نیمی از راهحلش را
فرستاده بود و قول داده بود که اگر 1000 مارک به او پیشپرداخت دهیم بقیه را نیز
برای ما میفرستد؛ یا اینکه دیگری قول داده بود که 1% درآمدی که از انتشار کتابها
و مصاحبههای مطبوعاتی که پس از مشهور شدن نصیب او خواهد شد را به من واگذار میکند،
و تهدید کرده بود اگر از او پشتیبانی نکنم او راه حل خودش را برای بخش ریاضی
دانشگاههای روسیه خواهد فرستاد تا افتخار آن نصیب آنها شود. گاهگاهی هم سر و کله
کسی در دانشگاه گوتینگن پیدا میشود و اصرار دارد بطور خصوصی درباره این موضوع با
او گفتگو کنیم.
تقریباً
همه ’راهحلها‘ در سطحی بسیار ابتدایی نوشته شدهاند (با استفاده از نمادگذاری
دبیرستانی و با رجوع به مقالات اثبات نشده در نظریه اعداد)، ولی بااینحال فهم آنها
میتوانند بسیار پیچیده باشد. از نظر اجتماعی فرستندگان این نامهها کسانی هستند
که غالباً تحصیلات فنی دارند ولی نتوانستهاند برای خودشان شغلی دست و پا کنند و
سعی دارند با اثبات مسئله فرما برای خودشان موفقیتی را حاصل کنند. من برخی از این
نامهها را به دکترهای روانشناس دادهام، و آنها نیز تشخیص دادهاند که فرستنده به
نوعی اسکیزوفرنی (schizophrenia)
حاد دچار است!
یکی از
خواستههای ولفسکل این بود که نتیجه این مسابقه بصورت سالیانه در یکی از نشریات
معتبر ریاضی چاپ شود. ولی تقریباً بعد از یک سال این نشریات بدلیل مواجه شدن با انبوهی
از نامههای پوچ و دیوانهوار از چاپ این نتایج سرباز زدند. امیدوارم این اطلاعات
برای شما جالب باشد.
اف. شیلیکتینگ
همانطور
که دکتر شیلیکتینگ اشاره میکند، رقابتکنندگان تنها خودشان را به فرستادن ’جواب‘
برای دانشگاه گوتینگن مقید نمیکنند. بخش ریاضی هر دانشگاهی احتمالاً گنجهای دارد
که پر از اثباتهای غیر حرفهای است. ولی اکثر موسسات چنین اثباتهای غیر حرفهای
را نادیده میگیرند.
هرچند ریاضیدانان آماتور در قرن
بیستم تلاش کردند برای آخرین قضیه فرما اثباتی را پیدا کنند و جایزه ولفسکل را
ببرند، ولی ریاضیدانان حرفهای عمدتاً به نادیده گرفتن این مسئله ادامه دادند. این ریاضیدانان بجای ادامه راه کومر و
دیگر متخصصین نظریه قرن-نوزدهم، شروع به کند و کاش درمورد ماهیت اعداد کردند. برخی
از بزرگترین چهرههای قرن بیستم، از جمله برتراند راسل (Bertrand Russell)، داوید هیلبرت، و کورت
گودل (Kurt Gödel) تلاش کردند به
ژرفترین خواص اعداد پی ببرند تا معنی واقعی آنها را درک کنند و ببینند در نظریه
اعداد به چه سئوالاتی میتوان جواب داد، و مهمتر از آن، به چه سئولاتی نمیتوان
جواب داد. کارهای آنها پایههای ریاضیات را تکان داد و سرانجام برای آخرین قضیه
فرما نیز پیآمدهایی دربرداشت.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
الگوهای
یک ریاضیدان باید مانند رنگهای یک نقاش یا واژههای یک شاعر زیبا باشند، آنها باید
بشکل همآهنگی در کنار هم قرار بگیرند. زیبایی شرط اول است؛ در جهان جایی برای
ریاضیات زشت وجود ندارد.
جی. اچ هاردی
در ژانویه
1954 یک ریاضیدان بااستعداد ژاپنی بنام گورو شیمورا (Goro Shimura) به کتابخانه گروه ریاضی
دانشگاه توکیو رفت. او بدنبال نسخهای از جلد 24 نشریه آلمانی ماتماتیش آنالن
(Mathematische Annalen) بود. خصوصاً او
بدنبال مقالهای از ماکس دورینگ (Max
Deuring) میگشت که درباره نظریه جبری ضربِ مختلط
(complex multiplication) بود، و او برای
محاسبات عجیب و پیچیده خودش به آن نیاز داشت.
در کمال
تعجب او متوجه شد که این جلد قبلاً از کتابخانه به امانت گرفته شده. کسی که آن را
به امانت گرفته بود یکی از آشنایان شیمورا بنام یوتاکا تانیاما (Taniyama Yutaka) بود که در آن سوی خوابگاه زندگی میکرد و خُلق عجبی
داشت. شیمورا یادداشتی را برای تانیاما فرستاد و برای او توضیح داد که او برای
محاسبات دشوار خودش به این جلد نیاز فوری دارد، و محترمانه از او پرسید که چه
زمانی مجله را بازمیگرداند. بعد از چند روز یک کارتپستال روی میز شیمورا قرار
گرفت. تانیاما در جواب او توضیح داده بود که او نیز دقیقاً درگیر همین محاسبات است
و در همین مرحله از کار گیر افتاده. او به شیمورا پیشنهاد کرد که آنها ایدههای
خودشان را با هم درمیان بگذارند و شاید بتوانند باهم روی مسئله کار کنند. اتفاقی
که بر سر قرض گرفتن یک مجله از کتابخانه رخ داد، نقطه شروع مشارکتی بود که بکلی
مسیر تاریخ ریاضیات را تغییر داد.
تانیاما
در 12 نوامبر سال 1927 در شهر کوچکی که چند مایل با توکیو فاصله داشت بدنیا آمد.
در کودکی تحصیلات تانیاما دائماً با وقفه روبرو بود. او مدت زیادی درگیری بیماریهای
مختلف بود، و در نوجوانی به سل مبتلا شده بود و برای دو سال نتوانست به دبیرستان
برود. شروع جنگ جهانی دوم وقفه بیشتری را در تحصیلات او بوجود آورد.
تحصیلات
گورو شیمورا، که یکسال از تانیاما کوچکتر بود، در طول سالهای جنگ کلاً متوقف شد.
مدرسه او بسته شده بود، و شیمورا بجای اینکه روزها درس بخواند مجبور بود با کار در
کارخانه ساخت قطعات یدکی هواپیما به جنگ یاری کند. او هر روز عصر تلاش میکرد تا
خودش دروس از دست رفته را فرا بگیرد. او بویژه به ریاضیات علاقه داشت، و در
اینباره چنین میگوید: ”البته موضوعات زیادی برای یادگیری وجود دارند، ولی ریاضیات
از بقیه راحتتر بود، زیرا برای اینکار تنها لازم بود که من کتابهای درسی ریاضی
را بخوانم. من حسابان را با کتاب خواندن یادگرفتم. اگر میخواستم رشته دیگری، مثل
شیمی یا فیزیک را دنبال کنم، آنگاه به تجهیزات علمی نیاز بود که من پولی برای خرید
آنها نداشتم. من هیچ وقت پیش خودم فکر نکردم که بااستعداد هستم، و فقط کنجکاو
بودم.“ چند سال پس از پایان جنگ، شیمورا و تانیاما وارد دانشگاه شدند. زمانی که
آنها بر سر آن نشریه با هم کارتپستال رد و بدل میکردند، زندگی در توکیو به روال
عادی خودش بازمیگشت و این دو دانشجوی جوان شروع به وقت گذرانی با یکدیگر کردند.
آنها بعد از ظهر خودشان را در کافیشاپها سپری میکردند، و شبها در رستوران کوچکی
شام میخوردند که در پخت گوشت نهنگ تخصص داشت، و آخر هفتهها هم یا به باغ گیاهشناسی
و یا به پارک شهر میرفتند. این مکانها جای ایدهالی برای بحث درباره تفکرات ریاضی
آنها بود.
هرچند
شیمورا رگهای از رفتار بوالهوسانه داشت – و حتی امروز هم طرفدار جُوکهای
بودایی است، ولی خلق و خوی او در مقایسه با شریکش بسیار معتدلتر بود. شیمورا
سپیده دم از خواب برمیخواست و فوراً شروع بکار میکرد، درحالی که همکارش اغلب
اوقات در آن موقع هنوز بیدار مانده بود و تمام شب را کار کرده بود. کسانی که به
آپارتمان تانیاما میرفتند میدیدند که او در بعد از ظهرها خواب کوتاهی میکند.
درحالی که
شیمورا سختگیر بود، تانیاما تا اندازه زیادی شلخته بود. عجیب بود که شیمورا این
خصوصیت او را تحسین میکرد: ”او بااستعداد بود و در اشتباه کردن تخصص ویژهای
داشت، ولی اشتباهات او در جهت درستی بودند. من برای این خصوصیتش به وی رشک میبردم
و تلاش میکردم از او تقلید کنم، ولی اینکه آدم اشتباهات خوبی را بکند، کار بسیار
دشواری است.“
تانیاما
نمونهای از یک انسان نابغه هواسپرت بود و این کاملاً در ظاهر او هویدا بود. او
نمیتوانست بندکفشهایش را درست گره بزند، و بنابراین تصمیم گرفت بجای اینکه چندبار
در روز کفشهایش را گره بزند، آنها را اصلاً گره نزند. او همیشه کت و شلوار سبزی را
میپوشید که برق متالیک عجیبی در آن بود. این لباس از پارچهای دوخته شده بود که
آنقدر زشت بود که بقیه اعضای خانواده از آن بدشان میآمد.
هنگامی که
برای اولین بار تانیاما و شیمورا در سال 1954 با هم ملاقات کردند، آنها در آغاز
کارشان بودند. رسم بر این بود، و هنوز هم هست، که محققین جوان تحت نظارت یک استاد
راهنما قرار بگیرند، ولی تانیاما و شیمورا این کارآموزی را نپذیرفتند. در طول
سالهای جنگ، تحقیقات واقعی ریاضی متوقف شده بود و حتی در طول دهه 1950 نیز هنوز
اعضاء هیاتهای علمی ریاضی بدرستی احیاء نشده بودند. بنا به گفته شیمورا همه
استادان ’خسته و ناامید‘ بودند. در مقایسه با دوران پیش از جنگ، دانشجویان اشتیاق
بیشتری برای یادگیری داشتند، و بزودی فهمیدند که تنها راهی که میتوانند سریعاً
پیشرفت کنند این است که خودشان به خودشان تعلیم دهند. دانشجویان مرتباً سمینارهای
مختلفی را ترتیب میدادند، و از آن طریق یکدیگر را از آخرین پیشرفتها و تکنیکهای
بدست آمده آگاه میکردند. وقتی پای این سمینارها به میان آمد، تانیاما برخلاف بیمیلیاش،
به نیروی محرکه عمدهای برای اینکار بدل شد. او دانشجویان ارشد را تشویق میکرد که
به اکتشاف سرزمینهای ناشناخته بپردازند و برای دانشجویان جوانتر بعنوان یک راهنما
عمل میکرد.
سمینارها
معمولاً موضوعاتی را پوشش میدادند که در اروپا و امریکا قدیمی محسوب میشدند. بیتجربگی
دانشجویان به این منجر میشد که آنها معادلاتی را مطالعه میکردند که در آن زمان
در غرب منسوخ شده بودند. یکی از این موضوعاتِ از مد افتاده، که هم تانیاما و هم
شیمورا را مجذوب خودش کرده بود، مطالعه فرمهای ماجولار (modular forms) بود.
فرمهای
ماجولار یکی از مرموزترین و عجیبترین اشیائی هستند که در ریاضیات وجود دارند. آنها
جزء عجیبترین نهادهای ریاضی هستند، بااینحال ریاضیدان آلمانی مارتین ایشلر
(Martin Eichler) آنها را جزء پنج عمل
اصلی ریاضی طبقه بندی میکند و میگوید ما پنج عمل داریم: جمع، تفریق، ضرب، تقسیم
و فرمهای ماجولار. بسیاری از ریاضیدانان خودشان را در چهار عمل اول متخصص میدانند،
ولی در مورد پنجمی آنقدرها مطمئن نیستند.
ویژگی اصلی فرمهای ماجولار در سطحِ تقارنِ غیرعادی
آنها است. هرچند بیشتر مردم با مفهوم روزمره تقارن آشنا هستند، ولی تقارن در
ریاضیات معنی بخصوصی دارد. شیئی دارای تقارن است که بتواند از طریق خاصی تبدیل
شود، ولی بااینحال پس از تبدیل بدون تغییر بنظر برسد. برای درک تقارنِ فوقالعاده
فرمهای ماجولار ابتدا باید تقارن اشیاء پیش و پا افتادهای همچون یک مربع ساده
را بررسی کنیم:
شکل 15. یک مربع ساده هم تقارن چرخشی دارد و هم تقارن
بازتابی.
برای یک
مربع، یکی از تقارنهای آن چرخشی است. این یعنی اگر ما
نقطهای را درنظر بگیریم که محور-x و محور-y همدیگر را قطع میکنند، آنگاه مربعی که در شکل 15 نشان داده
شده میتواند به اندازه یکچهارم دورکامل به دور این نقطه بچرخد، و پس از اینکار
بدون تغییر بماند و مانند قبل بنظر برسد. به همین نحو، چرخشهایی به اندازه نیم
دور، سه-چهارم دور، و یک دورکامل نیز در مربع هیچ تغییری بوجود نخواهند آورد.
علاوه بر تقارن
چرخشی (rotational symmetry)،
مربع دارای تقارن دیگری هم هست که تقارن بازتابی یا انعکاسی
(reflectional symmetry) نامیده میشود. اگر
ما آیینهای را تصور کنیم که در طول محور-x
قرار داده شده، آنگاه نیمه بالایی مربع دقیقاً نیمه پایینی آن را بازتاب میدهد، و
همینطور عکس آن، بنابراین مربع پس از این تبدیل بدون تغییر خواهد ماند. بطور مشابه
ما میتوانیم سه آیینه دیگر را طوری قرار دهیم که در آن مربع بازتاب داده شده با
مربع اولیه یکسان خواهد بود. یکی از این سه آیینه میتواند در طول محور-y، و دوتای دیگر میتوانند در دو قطر مربع قرار بگیرند.
مربع ساده هم تقارن چرخشی دارد و هم تقارن بازتابی،
و شکل نسبتاً متقارنی است، ولی هیچگونه تقارن انتقالی ندارد. این یعنی اگر مربع به
هر جهتی انتقال داده شود، ناظر فوراً متوجه این حرکت خواهد شد، زیرا موقعیت مربع
نسبت به محورها تغییر میکند. ولی اگر همانگونه که در شکل 16 نشان داده شده، کل
فضا با مربع فرش چین شده باشد، این مجموعه بینهایت از مربعها یک تقارن انتقالی
خواهد داشت. اگر چنین سطحِ بینهایتی به اندازه یک یا چند مربع به بالا یا به پایین
حرکت کند، آنگاه سطح انتقال داده شده با حالت اولیه یکسان خواهد بود.
شکل
16. سطحی که با بینهایت
مربع پوشانده شده، تقارن چرخشی و بازتابی را از خودش بروز میدهد و علاوه بر آن
دارای تقارن انتقالی نیز هست.
تقارن سطوحی که با کاشیهای مربعی پوشانده شده باشد
یک ایده نسبتاً ساده است، ولی مانند خیلی از مفاهیم ساده دیگر، ظرافتهای فراوانی
در پشت آن نهفته است. برای مثال، در دهه 1970 فیزیکدان و ریاضیدان انگلیسی راجر
پنرُز (Roger Penrose) کاشیهای مختلفی را
در یک سطح یکسان قرار دارد. نهایتاً او در میان آنها توانست دو شکل جالب را تشخیص
دهد، و آنها را بادبادک و پیکان نامید (به شکل 17 نگاه کنید). اگر از هر یک از
آنها به تنهایی استفاده شود، فقط به یک طریق میتوان از آنها برای پوشاندن سطح
استفاده کرد که در آن هیچگونه روزنه و یا رویهم افتادن در کار نباشد، ولی اگر از
هر دو آنها با هم استفاده شود، از آنها میتوانند برای ایجاد یک سری از الگوهای
کاشیکاری استفاده کرد. بادبادکها و پیکانها میتوانند به بینهایت شکل مختلف در
کنار یکدیگر قرار بگیرند، و گرچه همه این الگوها در ظاهر مشابه هستند، ولی در
جزئیات با هم متفاوتند. در شکل 17 یکی از الگوهایی که با استفاده از پیکانها و
بادبادکها ایجاد شده دیده میشود.
شکل
17. راجر پنرُز با
استفاده از کاشیهای مختلفی شبیه بادبادک و پیکان توانست یک سطح را بپوشاند. ولی
کاشیکاری پنرُز دارای تقارن انتقالی نیست.
یکی از
خصوصیات مهم دیگر کاشیکاری پنرُز (یعنی، الگوهایی که توسط کاشیهایی مثل پیکان و
بادبادک تولید شده) این است که آنها میتوانند سطح محدودی از تقارن را از خودشان
نشان دهند. در نگاه اول بنظر میرسد کاشیکاری که در شکل 17 نشان داده شده دارای
تقارن انتقالی است، ولی با اینحال هر تلاشی که در جهت حرکت دادن الگو به طرفین
انجام شود تا الگوی انتقال داده شده با الگوی اولیه یکی باشد، نهایتاً به شکست
منجر خواهد شد. الگوهای پنرُز بطور فریبندهای نامتقارن هستند، و به همین دلیل
است که توجه ریاضیدانان را به خودشان جلب کردهاند و به نقطه شروعی برای حوزه
جدیدی از ریاضیات بدل شدهاند.
کاشیکاری
پنرز در مهندسی مواد نیز کاربرد دارد. بلورشناسان همیشه براین باور بودهاند که بلورها
(crystals) باید براساس اصولی ساخته شده
باشند که در پشت کاشیکاری مربعی قرار دارد، یعنی دارای سطح بالایی از تقارن
انتقالی باشند. از لحاظ نظری، بلورها بر یک ساختار تکرارشونده و خیلی منظم تکیه
دارد. ولی در سال 1984 دانشمندان یک بلور فلزی را کشف کردند که از آلومینیم و
منگنز ساخته شده بود و با الگوهای پنرز منطبق بود. موزائیکی از آلومینیوم و منگنز
که مانند بادبادکها و پیکانها رفتار میکردند، و بلوری را میساخت که تقریباً منظم
بود، ولی نه بطور کامل. اخیراً یک شرکت فرانسوی نوعی از کریستال پنرُز را تولید
کرد که برای پوشاندن کف ماهیتابهها از آن استفاده میشود.
آنچه
درمورد سطوح کاشیکاری پنرُز جالب است، تقارن محدود آنهاست، درحالیکه خاصیت جالب
فرمهای ماجولار این است که آنها تقارنِ بینهایتی را از خودشان نشان میدهند. فرمهای
ماجولاری که از سوی تانیاما و شیمورا مورد مطالعه قرار گرفتند میتوانند به طرق
بینهایتی حرکت کنند، عوض شوند، بازتابانده شوند، چرخانده شوند، و بااینحال بدون
تغییر بمانند، و این باعث میشود آنها متقارنترین اشیاء ریاضی باشند. هنگامی که
علامه فرانسوی هنری پوانکاره (Henri
Poincaré) در اواخر قرن نوزدهم به مطالعه فرمهای ماجولار
پرداخت، در مورد تقارن بیاندازه آنها با مشکل فراوانی روبرو بود. پس از مطالعه
گونه خاصی از فرمهای ماجولار، او برای همکارانش شرح داد که چگونه هر روز به مدت
دو هفته صبحها خواب بیدار میشد و سعی میکرد اشتباهی را در محاسباتش پیدا کند.
او در روز پانزدهم متوجه این موضوع شد، و پذیرفت که فرمهای ماجولار حقیقتاً تقارن
بیاندازهای دارند.
متاسفانه
ترسیم، یا حتی تصور کردن، یک فرم ماجولار غیر ممکن است. درمورد کاشیکاری مربع، ما
شیئی را داشتیم که در دو بُعد زندگی میکرد، و فضای آن توسط دو محور x و y تعریف میشد. یک فرم ماجولار نیز توسط دو محور تعریف میشود، ولی محورهای آن
مختلط هستند، یعنی هر محور دارای یک جزء حقیقی و یک جزء موهومی است و عملاً به دو
محور تبدیل میشود. بنابراین اولین محورِ مختلط باید توسط دو محور نمایش داده شود،
محور-xr (حقیقی) و محور-xi (موهومی)، و محور دوم مختلط
نیز توسط دو محور نمایش داده میشود، محور-yr
(حقیقی) و محور-yi (موهومی). اگر بخواهیم
دقیقتر بگوییم، فرم ماجولار در نیم-صفحه بالایی این فضای مختلط قرار دارد، ولی
چیزی که اهمیت دارد این است که این یک فضای چهار-بعدی است که بصورت (xr, xi, yr, yi)
بیان میشود.
این فضای
چهار-بُعدی یک فضای هذلولی (hyperbolic
space) نامیده میشود. درک جهان هذلولی برای انسانهایی که در
یک جهان سه-بعدی معمولی محدود شدهاند دشوار است. ولی مفهوم فضای چهار-بُعدی از
لحاظ ریاضی معتبر است، و همین ابعاد اضافی هستند که به فرمهای ماجولار چنین سطح
بالایی از تقارن را میدهند. هنرمندی بنام موریس اِشر (Mauritz Escher) شیفته ایدههای ریاضی بود و
تلاش کرد تا از مفهوم فضای هذلولی در بعضی از طرحها و نقاشیهای خودش استفاده
کند. تابلو (Circle Limit IV) یک جهان هذلولی را
به نمایش میگذارد که در یک صفحه دو-بُعدی جاسازی شده.

نقاشی (Circle
Limit IV) اثر موریس اِشر
در یک
جهان واقعی هذلولی، شیاطین و فرشتگان اندازه یکسانی دارند، و تکرار آنها نشانه سطح
بالایی از تقارن است. گرچه برخی از این تقارنها میتواند در یک صفحه دو-بعدی دیده
شود، ولی هر چه به لبههای تصویر نزدیک شویم اعوجاج تصویر نیز بیشتر میشود.
فرمهای ماجولاری که در یک فضای هذلولی زندگی میکنند
به شکلها و اندازههای مختلفی هستند، ولی هر یک از آنها از اجزاء اساسی یکسانی
ساخته شده است. چیزی که هر فرم ماجولار را از دیگری متفاوت میکند تعداد اجزائی
است دربر دارد. اجزاء یک فرم ماجولار بصورت (M1, M2, M3, M4, …) از
یک تا بینهایت نامگذاری میشوند، و بنابراین یک فرم ماجولار خاص ممکن است حاوی یک
توده از جزء یک باشد (M1=1)،
سه توده از جزء دوم (M2=3)،
دو توده از جزء سوم (M3=2)،
و غیره باشد. اطلاعاتی که توصیف کننده چگونگی ساخت یک فرم ماجولار هستند را میتوان
در چیزی که به سریهای-ماجولار (modular
series)، یا سری-M،
معروف هستند خلاصه کرد. سری-M فهرستی است که
اجزاء تشکیل دهنده و مقدار لازم از هر کدام را نشان میدهد:
همانگونه
که سری-E
برای معادلات بیضوی حکم DNA آنها را دارد، سری-M نیز برای فرمهای ماجولار حکم DNA را دارد. مقدار هر
جزء که در سری-M فهرست شده حیاتی است.
بسته به اینکه شما چطور این مقادیر را تغییر میدهید، مثلاً اولین جزء را، ممکن
است شما یک فرم ماجولار متفاوت را بگیرید، که به همان میزان متقارن است، یا ممکن
است شما شیء جدیدی را تولید کنید که یک فرم ماجولار نباشد. اگر مقدار هر جزء به
دلخواه انتخاب شود، آنگاه احتمالاً شیئی که از آن حاصل میشود تقارن کمی دارد یا
اصلاً تقارنی ندارد.
فرمهای
ماجولار در ریاضیات جایگاه خاص خودشان را دارند. بویژه بنظر میرسد آنها ارتباطی
با اشیایی که وایلز در کمبریج آنها را مطالعه میکرد، یعنی معادلات بیضوی، ندارند.
فرمهای ماجولار موجودات پیچیدهای هستند که در قرن نوزدهم کشف شدند و عمدتاً
بدلیل تقارنی که داشتند مورد مطالعه قرار گرفته بودند. از سوی دیگر قدمت معادلات
بیضوی به یونان باستان بازمیگردد و ارتباطی با تقارن ندارند. در جهان ریاضیات،
فرمهای ماجولار و معادلات بیضوی در نواحی کاملاً متفاوتی زندگی میکنند، و هیچ کس
باور نداشت که کوچکترین ارتباطی میان این دو موضوع باشد. تانیاما و شیمورا با مطرح
کردن این بحث که فرمهای ماجولار و معادلات بیضوی در اصل یکی هستند، جامعه ریاضی
را تکان دادند. این دو ریاضیدانِ مستقل عقیده داشتند که میتوانند جهان ماجولار و
بیضوی را با هم متحد کنند.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
یک مسئله
حلکنِ خبره باید دو خصوصیت ناسازگار را باهم داشته باشد- یعنی هم یک تخیل پویا داشته
باشد، و هم یک سرسختی صبورانه.
هوارد وینتلی اِوز
”یک روز
تابستان 1986 بود و در منزل یکی از دوستانم مشغول نوشیدن چای سرد بودیم. در وسط
صحبت او بطور ناگهانی به من گفت که کن ریبت ارتباط میان تانیاما-شیمورا و آخرین
قضیه فرما را اثبات کرده. من مثل برقگرفتهها شده بودم. من میدانستم که از آن
زمان به بعد مسیر زندگیم تغییر میکند، زیرا این یعنی که من برای اثبات آخرین قضیه
فرما فقط مجبور بودم حدس تانیاما-شیمورا را اثبات کنم. این یعنی حالا رویای کودکی
من آنقدر محترم بود که روی آن کار شود. من میدانستم که هرگز نمیتوانم آن را رها
کنم. میدانستم که به خانه میروم و روی حدس تانیاما-شیمورا کار خواهم کرد.“
بیش از دو
دهه از زمانی که اندرو وایلز آن کتاب الهام بخش را در کتابخانه محلی خوانده بود میگذشت،
ولی حالا برای اولین بار او میتوانست مسیری را ببیند که به تحقق رویای کودکی او
ختم میشد. وایلز در مورد اینکه چگونه نظرش درباره حدس تانیاما-شیمورا ناگهان
تغییر کرد را اینطور بخاطر میآورد: ”یادم هست زمانی یکی از ریاضیدانان درمورد حدس
تانیاما-شیمورا چیزی نوشته بود، و با گستاخی از آن بعنوان یک تمرین برای کسانی یاد
کرده بود که علاقهمند هستند. خوب، فکر میکنم در آن موقع من دیگر علاقهمند شده
بودم!“
وایلز پس
از اینکه زیر نظر پرفسور کوتز تز دکترایش را تمام کرد، به دانشگاه پرینستون رفت و
حالا خودش آنجا استاد بود. به لطف راهنماییهای کوتز، حالا وایلز احتمالاً بیش از
هر کس دیگری در دنیا درباره معادلات بیضوی اطلاع داشت، ولی او میدانست که با وجود
اینهمه دانش و مهارتهای ریاضی که دارد، بازهم کاری که در پیشرو دارد بسیار عظیم
است.
بسیاری از
ریاضیدانان، از جمله کوتز، عقیده داشتند که درگیر شدن در اثبات این حدس کار بیهودهای
است: ”من خودم شک داشتم که ارتباطِ زیبایی که میان آخرین قضیه فرما و حدس
تانیاما-شیمورا وجود دارد واقعاً به چیز خاصی منتهی شود، زیرا، باید اعتراف کنم
فکر نمیکردم اثبات حدس تانیاما-شیمورا قابل حصول باشد، و بازهم باید اعتراف کنم که
فکر نمیکردم تا من زندهام این حدس اثبات شود.“
وایلز از
موانع بسیاری که در پیش راه او بود آگاه بود، ولی حتی اگر او در راه اثبات آخرین
قضیه فرما شکست هم میخورد، او حس میکرد که تلاشهایش بیهوده نبودهاند: ”البته
سالها بود که حدس تانیاما-شیمورا مطرح بود. هیچ کس نمیدانست که با چه رویکردی
باید به آن نزدیک شد، ولی حداقل حالا جزئی از روند اصلی ریاضیات معاصر بود. من میتوانستم
برای اثبات آن تلاش کنم، و حتی اگر نمیتوانستم کار را تمام کنم، بازهم ریاضیات
باارزشی را تولید کرده بودم. من حس نمیکردم که وقتم را هدر دادهام. بنابراین عشق
فرما، که تمام عمر با من بود، حالا با یک مسئله حرفهای قابل قبول ترکیب شده
بود.“
در ابتدای
قرن بیستم از ریاضیدان بزرگ آلمانی داوید هیلبرت سئوال شد که چرا او هرگز تلاشی
برای اثبات آخرین قضیه فرما نکرده. او در جواب گفت: ”قبل از اینکه اینکار را شروع
کنم، باید سه سال از وقتم را صرف مطالعه موضوعاتی میکردم که به آن مربوط بود. من
چنین وقتی نداشتم تا آن را بر روی مسئلهای هدر دهم که احتمالاً به شکست میانجامد.“
وایلز میدانست برای اینکه امیدی به یافتن یک اثبات داشته باشد او ابتدا باید خودش
را غرقِ این مسئله کند، ولی برخلاف هیلبرت، او آماده این مخاطره بود. او تقریباً
تمام مقالات اخیر را خوانده بود و بارها و بارها آخرین تکنیکها را امتحان کرده
بود. وایلز، که تمام سلاحهای لازم برای نبرد را جمع آوری کرده بود، باید هجده ماه
وقت صرف میکرد تا خودش را با ریاضیاتی آشنا کند که تا کنون در مورد معادلات بیضوی
و یا فرمهای ماجولار بکار گرفته شده، یا از آنها منتج شده بود. اینکار سرمایهگذاری
نسبتاً بیخطری بود، زیرا او انتظار داشت هرگونه تلاش جدی برای اثبات این حدس
حداقل میتوانست ده سال بطول بیانجامد.
وایلز
تمام فعالیتهای خودش را که با اثبات آخرین قضیه فرما بصورت مستقیم ارتباط نداشتند
را کنار گذاشت، و از شرکت در سمینارها و کنفرانسهایی که هرگز تمامی نداشتند سرباز
زد. بدلیل اینکه وایلز هنوز در بخش ریاضی دانشگاه پرینستون مسئولیتهای را داشت، او
به شرکت در سمینارهایی که در آنجا برگذار میشد و نیز آموزش دانشجویان دوره لیسانس
ادامه داد. تا آنجا که امکان داشت او از مشغولیاتی که یک عضو هیئت علمی داشت دوری
میکرد و در خانه میماند تا در اطاق خلوت خودش در انزوا کار کند. به امید اینکه
بتواند راهبردی را برای حمله به مسئله تانیاما-شیمورا پیدا کند، او در اطاق خلوت
خودش تلاش میکرد تا قدرت تکنیکهای موجود را گسترش دهد.
او
دراینباره میگوید: ”من عادت داشتم به اطاق کارم در طبقه بالا بروم، و تلاش کنم تا
الگوهایی را پیدا کنم. من سعی کردم محاسباتی را انجام دهم که که تکه کوچکی از
ریاضیات را توضیح میداد. من سعی کردم آن را با درک مفهوم گستردهای وفق دهم
که قبلاً در بعضی از بخشهای ریاضیات وجود داشت و میتوانست مسئله خاصی که من روی
آن فکر میکردم را روشن کند. برخی اوقات این شامل جستجو در یک کتاب میشد تا ببینم
آنجا اینکار چطور انجام شده. برخی اوقات هم این شامل دستکارهای مختصری میشد، و به
محاسبات بیشتری نیاز داشت.“
از لحظهای
که وایلز قدم در راه اثبات گذاشت، تصمیم مهمی را گرفت و آن این بود که در انزوا و
مخفیانه کار کند. در ریاضیات معاصر نوعی فرهنگ همکاری و تشریک مساعی برقرار بود،
بنابراین تصمیم وایلز نوعی بازگشت به دوران گذشته بود. گویی اینکار تقلیدی از منش
خود فرما، یعنی بزرگترین ریاضیدان گوشه نشین دنیا، بود. وایلز توضیح میدهد که
بخشی از دلیلی که میخواست بطور مخفیانه کار کند این بود که حواسش پرت نشود: ”من
متوجه شدم که هر چیزی که با آخرین قضیه فرما مرتبط باشد توجه زیادی را بخودش جلب
میکند. شما نمیتوانید برای سالها تمرکز داشته باشید، مگر اینکه واقعاً حواستان
را روی مسئله مورد نظر متمرکز کنید، و اگر ناظرانِ زیادی نظارهگر کار شما باشند،
این تمرکز از دست میرود.“
انگیزه
دیگری که وایلز برای این نهانکاری داشت، باید به افتخار طلبی او ربط داشته باشد.
او از این هراس داشت که وضعیتی پیش بیاید که او بیشتر کارهای مربوط به اثبات را
انجام داده باشد و فقط قسمت کوچکی از آن ناتمام بماند. در اینصورت اگر اخبار
پیشرفتهای او به بیرون درز کند، هیچ چیزی نمیتواند مانع این شود که ریاضیدانانِ
رقیب دست بکار شوند و با تکمیل اثبات، اعتبار حل مسئله را نصیب خودشان کنند.
وایلز در سالهای آتی کشفیات خارقالعادهای را انجام
میداد، که هیچ یک از آنها تا وقتی بطور کامل اثبات نشدهاند، نه در جایی مورد بحث
قرار میگرفتند و نه منتشر میشدند. حتی نزدیکترین همکاران او هم از تحقیقات او
چیزی نمیدانستند. جان کوتز روزی را بخاطر دارد که با وایلز صحبت میکرد و او هیچ
نشانهای از اینکه مشغول چه کاری است از خودش بروز نداده بود. او میگوید: ”یادم
هست که چند دفعه به او گفتم ’این رابطهای که میان آخرین قضیه فرما و حدس
تانیاما-شیمورا پیدا شده خیلی جالبه، ولی فکر نمیکنم هنوز کسی بتونه این حدس را
ثابت کنه.‘ تصور میکنم او با شنیدن این حرف فقط لبخند زد.“

جان کوتز (John Coates)
-1945. استاد راهنمای وایلز.
کن ریبت،
که ارتباط میان آخرین قضیه فرما و حدس تانیاما-شیمورا را کامل کرده بود، نیز بکلی
از فعالیتهای مخفی وایلز بیخبر بود. او میگوید: ”احتمالاً این تنها موردی است که
خبر دارم کسی برای چنین مدت طولانی مشغول کار بر روی مسئلهای بوده، آنهم بدون
اینکه از کاری که میکند، یا پیشرفتهایی که حاصل کرده، چیزی را بروز دهد. از نظر
من چنین چیزی سابقه نداشته. در جامعه ما [ریاضیدانان]، مردم همیشه ایدههای
خودشان را با هم درمیان میگذارند. ریاضیدانان در کنفرانسها دور هم جمع میشوند،
آنها در سمینارها به ملاقات هم میروند، برای یکدیگر ایمیل میفرستند، پشت تلفن
باهم صحبت میکنند، از هم نظر میخواهند- ریاضیدانان همیشه با هم در ارتباط هستند.
وقتی شما با کس دیگری صحبت میکنید از طرف آنها نوازش میشوید؛ آنها به شما میگویند
که کاری که کردهاید چقدر باارزش است، آنها به شما ایده میدهند. این نوعی تغذیه
است و اگر خودتان را از آن محروم کنید، آنگاه کاری را میکنید که از نظر روانی
بسیار عجیب است.“
وایلز
برای اینکه سوء ظن همکارانش را برنیانگيزد تمهید ماهرانهای را ابداع کرد. او در
اوایل دهه 1980 بر روی تحقیق عمدهای کار میکرد که با نوع خاصی از معادلات بیضوی
رابطه داشت، و قصد داشت آن را بطور کامل منتشر کند. ولی وقتی کشفیات ریبت و فرآی
منتشر شدند، نظرش را تغییر داد. وایلز تصمیم گرفت که نتیجه تحقیقاتش را اندک اندک
منتشر کند، و اینکار را هر شش ماه یکبار انجام دهد. این تحقیقِ ظاهری همکارانش را
قانع میکرد که او هنوز درگیر کارهای قبلی خودش است. تا وقتی وایلز این بازی را
ادامه میداد، میتوانست بدون اینکه هیچ یک از پیشرفتهای خودش را بروز دهد، به
دغدقه اصلی خودش بپردازد.
تنها کسی
که از کارهای مخفی وایلز اطلا داشت، همسرش نادا (Nada)
بود. درست بعد از اینکه وایلز کارش را بر روی اثبات شروع کرد، آنها با هم ازدواج
کردند، و همانطور که محاسبات او ادامه داشت تنها کسی که رازدار او بود نادا بود.
تنها چیزی که در سالهای آتی مایه سرگرمی وایلز میشد خانواده او بود. ”تنها کسی که
از کارهای من درباره آخرین قضیه فرما خبر داشت همسرم بود. چند روز بعد از
عروسیمان، وقتی با هم به ماهعسل رفته بودیم من این را به او گفتم. البته همسرم
قبلاً درمورد آخرین قضیه فرما شنیده بود، ولی در آن موقع او از اهمیت عاشقانهای
که این مسئله میتواند برای یک ریاضیدان داشته باشد هیچ اطلاعی نداشت، و نمیدانست
که این مسئله چقدر میتواند زندگی ما را برای سالها دشوار کند.“
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
مسئلهای
که ارزش حل کردن داشته باشد، ارزش خودش را با چالشطلبی نشان میدهد.
پیت هین (Piet Hein)
به محض
اینکه درسهای کمبریج به پایان رسید، کمیته ولفسکل از اثبات وایلز مطلع شد. آنها نمیتوانستند
فوراً جایزه را اهدا کنند، زیرا قواعد مسابقه بطور وضوح حکم میکرد که اثبات باید
توسط ریاضیدانان دیگر و همچنین ناشران رسمی مورد تایید قرار گیرد:
کمیته
دانشگاه گوتینگن فقط آن دسته از مقالات را درنظر خواهد گرفت که بصورت یک رساله در
یکی از نشریات دورهای، یا بصورت کتاب در کتابفروشیها موجود باشند... اهداء جایزه
توسط انجمن به هیچ وجه در زمانی کمتر از دو سال از هنگام چاپ مقاله انجام نخواهد
شد. این فاصله زمانی به این منظور درنظر گرفته شده تا ریاضیدانان آلمانی و خارجی
فرصت داشته باشند که نظر خودشان را در مورد اعتبار حل این مسئله بیان کنند.
وایلز
مقاله خودش را برای نشریه Inventiones Mathematicae
فرستاده بود، که درنتیجه ویراستار آن بَری میزِر شروع به انتخاب هیت داوران نمود.
مقاله وایلز شامل طیف گستردهای از تکنیکهای جدید، و حتی قدیمی، بود و به
همین دلیل میزر تصمیم گرفت بجای دو یا سه داور، شش داور را برای بررسی آن انتخاب
کند. هر ساله در سراسر دنیا سی هزار مقاله در نشریات مختلف چاپ میشوند، ولی حجم
زیاد و اهمیتی که مقاله وایلز داشت به این معنی بود که سطح بررسی آن نسبت به بقیه
متفاوت خواهد بود. اگر بخواهم ساده بگویم، اثبات 200-صفحهای او به شش بخش تقسیم،
و هر داور مسئول بررسی هر یک از این بخشها شد.
مسئول بخش
سوم نیک کَتز بود، که قبلاً همین بخش از اثبات وایلز را بررسی کرده بود. او
دراینباره میگوید: ”تابستان بود و من آن موقع برای انجام کاری در مؤسسه مطالعات علمی
پیشرفته در پاریس بودم. من متنِ کامل 200-صفحهای را با خودم داشتم- بخشی که مربوط
به خود من بود حدود 70 صفحه بود. هنگامی که به پاریس رسیدم تصمیم گرفتم تا کمی کمک
بگیرم. بنابراین اصرار کردم که لوک ایلوزی (Luc
Illusie)، که او نیز در پاریس بود، بعنوان داور کمکی در این بخش
همکار من باشد. ما در طول آن تابستان چندبار در هفته با هم ملاقات داشتیم، و سعی
میکردیم با درس دادن به یکدیگر این فصل را بهتر درک کنیم. اگر بخواهم دقیقتر
بگویم، تنها کاری که ما میکردیم نگاه کردن به خط خط این مقاله بود و تلاش میکردیم
مطمئن شویم که هیچ اشکالی در آنها نیست. بعضی وقتها ما چنان گیج میشدیم که من هر
روز، و بعضی وقتها روزی دو بار به اندرو ایمیل میفرستادم و از او در مورد فلان
صفحه یا فلان خط توضیح میخواستم. معمولاً من همان روز یا فردای آن روز پاسخی را
میگرفتم که در آن موضوع روشن شده بود، و پس از آن ما میتوانستیم به مرحله بعدی
برویم.“
استدلالات
این اثبات بسیار عظیم بودند. استدلالاتی که بطور پیچیدهای از صدها محاسبه ریاضی
ساخته شده بود و توسط هزاران پیوند منطقی به هم متصل شده بودند. اگر فقط یکی از
این محاسبات اشکال داشت، یا اگر فقط یکی از پیوندها سست میشد، آنگاه کل اثبات
بطور بالقوه بیارزش بود. وایلز، که حالا به پرینستون بازگشته بود، مضطربانه در
انتظار نتایج کمیته داوری بود. ”من تا وقتی بطور کامل از این مقاله راحت نشدهام
دوست نداشتم جشن بگیرم. ضمناً با سئوالاتی که داوران از طریق ایمیل برایم میفرستادند
هیچ وقتی برایم نمیماند. من هنوز اطمینان داشتم که هیچ یک از این سئوالات نمیتواند
یک مشکل جدی را بوجود آورد.“ او قبلاً خودش پیش از اینکه مقاله را به داوران بدهد
بارها اثبات را بررسی کرده بود، بنابراین انتظار داشت که اگر هم اشکالی در آن
باشد، این اشکالات معادل غلطهای دستوری و املایی یک نوشته معمولی باشد، چیزهایی
که بتواند سریعاً آنها را تصحیح کند.
کَتر آن
روزها را اینطور بخاطر میآورد: ”این سئوالات بیاینکه چیز مهمی در آنها باشد تا
ماه آگوست ادامه داشتند، تا اینکه من چیزی را پیدا کردم که بنظر کمی مشکلساز میآمد.
در 23 آگوست من به اندرو ایمیلی را فرستادم، ولی چون جواب آن کمی پیچیده بود و نمیشد
آن را از طریق ایمیل فرستاد، او جواب را از طریق فکس برایم فرستاد. ولی بنظر نمیرسید
که این فکس هم پاسخگوی مشکل باشد، بنابراین من دوباره ایمیل دیگری را فرستادم، که
او باز هم در جواب فکس دیگری را فرستاد که من هنوز از آن قانع نشده بودم.“
وایلز فکر
میکرد که این خطا نیز مانند بقیه موارد سطحی باشد، ولی اصرار کَتز او را وادار
کرد که آن را جدی بگیرد. وایلز در اینباره میگوید : ”من نمیتوانستم این سئوال
بظاهر ساده را فوراً حل کنم. تا مدتی اهمیت این سئوال هم مانند بقیه بنظر میرسید،
ولی در 11 سپتامبر من متوجه شدم که این یک مشکل کوچک نیست بلکه یک اشکال عمده است.
این اشکالی بود که در بخش مهمی از استدلال قرار داشت و به روش کولیواگین-فلاک
مربوط بود، ولی چنان ظریف بود که من تا آن موقع متوجه آن نشده بودم. این اشکال
چنان جنبه انتزاعی دارد که حقیقتاً نمیتوان آن را به زبان ساده توضیح داد. حتی
توضیح آن به زبان ریاضی هم ایجاب میکند که یک ریاضیدان دو یا سه ماه از وقت خودش
را صرف مطالعه دقیق آن بخش از مقاله بکند.“
مشکل اصلی
این بود که هیچ تضمینی وجود نداشت که روش کولیواگین-فلاک آنطور که وایلز انتظار
داشت جواب دهد. فرض بر این بود که میتوان اثبات را از اولین عضو همه معادلات
بیضوی و فرمهای ماجولار شروع کرد و آن را به همه عضوها بسط داد، که همانطور که
قبلاً توضیح داده شد، این واژگونسازیهای بعدی را فراهم میکرد. در ابتدا روش
کولیواگین-فلاک تنها در شرایط محدودی جواب میداد، ولی وایلز آن را طوری تعدیل
کرده بود که قدرتمندتر شود و برای کلیه نیازهای او جواب دهد. بر طبق نظر کَتز،
لزوماً چنین چیزی درست نبود و تاثیر چنین چیزی مصیبتبار و ویرانگر بود.
این خطا
لزوماً به معنی این نبود که نمیشد کار وایلز را نجات داد، ولی به این معنی بود که
او میباید استدلال خودش را قویتر میکرد. مطلقگرایی ریاضی حکم میکرد که وایلز
باید کلیه شبهات را رفع کند و روش او برای هر عضو از تمام سریهای-E و سریهای-M جواب دهد.
وقتی کَتز
به اهمیت خطایی که پیدا کرده پی برد، او شروع کرد تا از خودش این سئوال را بپرسد
که چرا در بهار هنگامی که با وایلز جلسه داشتند متوجه این خطا نشد. ”فکر میکنم
جواب این باشد وقتی شما درحال گوش دادن به یک درس باشید، تا اینکه آن را با آرامش
مطالعه کنید، تفاوت وجود دارد، زیرا در حالت اول تنش بیشتری وجود دارد. اگر شما هر
بار بخواهید با گفتن اینکه من فلان نکته را درست نمیفهم جریان درس را قطع کنید،
آن موقع مدرس هیچ وقت نمیتواند همه چیز را توضیح دهد و شما بجای نمیرسید. از سوی
دیگر اگر شما هیچ وقت حرف مدرس را قطع نکنید و فقط در تصدیق سخنان او سرتان را
تکان دهید، در این حالت نیز شما مسئله را بصورت درست نفهمیدهاید و آخر سر برخی از
اشکالات احتمالی از دستتان در میروند.“
تنها چند
هفته پیشتر روزنامهنگاران سراسر دنیا از وایلز بعنوان بااستعدادترین ریاضیدان
جهان یاد میکردند، که توانسته بعد از 350 سال معمای لاینحلی را حل کند که هیچ کس
از عهده حل آن برنیامده. ولی حالا وایلز با تحقیر روبرو بود و باید قبول میکرد
اشتباهی را مرتکب شده. او پیش از اینکه به این اشتباه اعتراف کند تصمیم گرفت با
تلاشی متمرکز، شکاف موجود را پر کند. ” نمیتوانستم تسلیم شوم. من با این مسئله
درگیر بودم و هنوز باور داشتم که روش کولیواگین-فلاک فقط نیاز به یک وصله کوچک
دارد. من باید اصلاح کوچکی را بر روی آن اعمال میکردم، که پس از آن بخوبی جواب میداد.
من تصمیم گرفتم دوباره به حالت قبلی خودم بازگردم و ارتباط خودم را بکلی با جهان
خارج قطع کنم. من باید دوباره حواس خودم را جمع میکردم، ولی اینبار تحت شرایط سختتری.
برای مدتی طولانی فکر میکردم اصلاح در دسترس بود، و من تنها چیز سادهای را از
قلم انداختهام که روز بعد آن را سرجایش میگذارم. البته میتوانست اینطور
باشد، ولی زمان میگذشت و بنظر میرسید که مشکل به قوت خودش باقی است.“
امید این
بود که او بتواند تا پیش از اینکه جامعه ریاضی بفهمد که اصلاً اشکالی وجود دارد آن
را برطرف کند. همسر وایلز که قبلاً شاهد هفت سال تلاش او برای اثبات این قضیه بود،
حالا باید شاهد این میبود که شوهرش باید دوباره با خطایی کلنجار برود که میتواند
همه چیز را نابود کند. وایلز درباره خوشبینی همسرش چنین میگوید: ”نادا در ماه
سپتامبر به من گفت تنها چیزی که برای تولدش میخواهد یک اثبات صحیح است. روز تولد
او 6 اکتبر بود، و من تنها دو هفته وقت داشتم که یک اثبات کامل را به او بدهم، و
در اینکار ناکام ماندم.“
آن زمان
برای نیک کَتز نیز دوره پرتنشی بود: ”تا ماه اکتبر، تنها کسانی که در مورد این خطا
اطلاع داشتند من، ایلوزی، داوران بخشهای دیگر، و خود اندرو بودند. روش من بعنوان
یک داور این بود که باید راز دار باشم. قطعاً این حس را داشتم که هیچ مسئولیتی
ندارم که این مسئله را به غیر از اندرو با کس دیگری درمیان بگذارم، بنابراین حتی
یک کلمه هم در مورد آن حرف نزدم. فکر میکنم رفتار او عادی بود ولی در این مرحله
او چیزی را از بقیه دنیا مخفی نگاه داشته بود، و فکر میکنم از این نظر خیلی
ناراحت بود. روش اندرو این بود که او میتواند تا یک روز دیگر این اشکال را برطرف
کند، ولی همینطور که پاییز به پایان میرسید و هیچ مقالهای عمومی هم بیرون نیامده
بود، شایعاتی پخش شد که در آنها از وجود یک مشکل صحبت میشد.“
به ویژه
کن ریبت، که یکی دیگر از داوران بود، از بابت این رازداری فشار زیادی را بر دوش
خودش احساس میکرد. او دراینباره میگوید: ”به دلایل کاملاً اتفاقی من به مسئول
روابط عمومی این مسئله بدل شده بودم. در آن موقع مقالهای در روزنامه نیویورک
تایمز چاپ شده بود و اندرو از من خواست که بجای او من با خبرنگار صحبت کنم، و
به همین دلیل در عنوان مقاله هم آمده بود ’ریبت که بعنوان سخنگوی وایلز عمل میکند
...‘. بعد از آن بود که هر موقع هر کس، چه در داخل جامعه ریاضی و چه خارج از آن،
میخواست اطلاعی درمورد آخرین قضیه فرما کسب کند به من مراجعه میشد. مردم از
روزنامهها، از همه جا، تماس میگرفتند و در مورد این قضیه سئوال میکردند. خود من
هم در طول یک دوره دو سه ماهه درسهای سنگینی را داشتم. در این درسها من به اهمیت
این دستآورد تاکید داشتم و خطوط اصلی اثبات، و آن بخشی که بهتر از بقیه میشناختم
را تشریح میکردم. ولی بعد از مدتی صبر مردم لبریز شد و شروع به پرسیدن سئوالات
ناجوری کردند.
” کاری که
وایلز در ابتدا انجام داد این بود که بطور عمومی اثبات این قضیه را اعلام کرد، ولی
در واقع هیچ کس بجز گروه معدودی از هیئت داوران متن این اثبات را در دست نداشتند.
بنابراین ریاضیدانان انتظار داشتند که یک کپی از این اثبات، که اندرو چند هفته پیش
قول آن را داده بود، در اختیار آنها قرار گیرد. مردم میگفتند ’خیلی خوب، حالا که
این قضیه اثبات شده ما میخواهیم ببینیم موضوع از چه قرار است، و او چه کرده؟ چرا
ما در اینمورد چیزی نمیشنویم؟‘ مردم از اینکه چرا آنها در جریان نیستند کمی نارحت
بودند و فقط میخواستند بدانند چه خبر است. بدلیل ابهامی که در بخشی از اثبات پیش
آمده بود، اوضاع بتدریج بدتر هم شد و مردم درباره شایعاتی که درباره شکاف در بخش
سوم بود با من صحبت میکردند. آنها از من سئوال میکردند که در اینمورد چه میدانم،
و من هم نمیدانستم چه جوابی باید بدهم.“
با اظهار
بیاطلاعی وایلز و هیئت داوران از وجود یک شکاف، یا حداقل عدم اظهار نظر درباره آن،
گمانهزنیهای زیادی به میان آمد. ریاضیدانان از روی ناچاری شروع به فرستادن ایمیل
برای یکدیگر کردند تا شاید بفهمند اوضاع از چه قرار است.
در چایخوری
بخش ریاضی تمام دانشگاهها شایعاتی در مورد اثبات وایلز مطرح میشد. در پاسخ به
شایعاتی که از طریق ایمیل پخش میشد، برخی از ریاضیدانان بقیه را به آرامش دعوت میکردند.
علیرغم
دعوت به آرامش، فرستادن ایمیلها بیوقفه ادامه داشت. حالا علاوه بر صحبت درباره
خطایی که در اثبات وجود داشت، برخی نیز از بیتفاوتی هیئت داوران گله داشتند.
درحالیکه
هیجانی که درباره این اثبات وجود داشت درحال فزونی بود، وایلز حداکثر تلاش خودش را
کرد که خودش را از این جنجالها و گمانهزنیها بدور نگاه دارد. او دراینباره میگوید:
”بدلیل اینکه نمیخواستم بدانم که مردم درباره من چه میگویند، حقیقتاً خودم را
منزوی کردم. من بیشتر وقتها در انزوا بودم ولی گاهگاهی همکارم پیتر سارناک
(Peter Sarnak) به من میگفت ’خودت
میدانی که بیرون چه طوفانی برپاست.‘ من هم گوش میدادم، ولی بخاطر خودم هم که بود،
برای اینکه بر روی مسئله تمرکز کنم، واقعاً میخواستم تنها باشم.“
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
اینبار
هیچ تردیدی درمورد اثبات وایلز وجود نداشت. دو مقاله، که رویهم رفته 130 صفحه
بودند، بیش از هر مقاله دیگری در تاریخ ریاضیات از سوی ریاضیدانان مورد بررسی دقیق
قرار گرفتند و سرانجام در ماه می 1995 متن کامل آنها در نشریه معتبر Annals of Mathematics چاپ شد.
بار دیگر
نام وایلز روی صفحه اول روزنامه نیویورک تایمز نقش بست. عنوان مقاله این بود:
’ریاضیدانان اعلام کردند که معمای دیرین حل شده.‘ ولی این مقاله تحتالشعاع موضوع
علمی دیگری قرار گرفته بود که عنوان آن این بود: ’یافتههای تازه درباره سن جهان
سئوالات جدیدی را درمورد کیهان مطرح کرده‘. هرچند اینبار روزنامهنگاران
علمی هیجان سابق را نسبت به آخرین قضیه فرما نداشتند، ولی از اهمیت این اثبات برای
ریاضیدانان اصلاً کاسته نشده بود. جان کوتز در اینباره گفت: ” یافتن اثبات نهایی
این قضیه در جهانِ ریاضیات معادل شکافتن اتم یا یافتن ساختار DNA است. اثبات آخرین قضیه فرما پیروزی بزرگی است که بدلیل
انقلابی که در نظریه اعداد بوجود آورده، هیچ کس نباید اهمیت آن را دست کم بگیرد.
از نظر من زیبایی و فریبندگی کار اندرو پیشرفت فاحشی در نظریه اعداد محسوب میشود.“
در طول
هشت سال تلاش سخت، وایلز تقریباً کلیه دستآوردهای مهمی که در قرن بیستم در زمینه
نظریه اعداد حاصل شده بود را در یک اثبات عظیم گرد هم جمع کرده بود. او تکنیکهای
ریاضی کاملاً جدیدی را درست کرده بود و آنها را با تکنیکهای سنتی به شکلی درهم
آمیخته بود که قبلاً هیچ وقت امکان آن میسر نبود. او با این کار خطوط جدیدی را
برای یورش به بسیاری از مسائل دیگر باز کرد. بر طبق گفته کن ریبت، این اثباتی است
که از ریاضیاتِ نوین ساخته شده و الهامبخش ریاضیاتِ آینده است: ” اگر شما در یک
جزیره دور افتاده گم شوید و فقط این مقاله را داشته باشید، فکر میکنم تا مدتها
بتواند غذای فکری شما را فراهم کند. شما میتوانید در آن تمام ایدههای جاری نظریه
اعداد را ببینید. همینطور که صفحات آن را ورق میزنید، بطور کوتاهی به برخی از
قضایای بنیادی دلین (Deligne)
بر میخورید، و ناگهان در صفحه بعد سر و کله قضیهای از هِلهگوراک (Hellegouarch) پیدا میشود و همه آنها
بخوبی نقش خودشان را بازی میکنند.“
درحالیکه
روزنامهنگاران علمی اثبات وایلز برای آخرین قضیه فرما را تحسین میکردند، ولی
تعداد اندکی از آنها به حدس تانیاما-شیمورا اشاره میکردند، حدسی که بطور جداییناپذیری
به این قضیه ربط داشت. آنها به خودشان زحمت نمیدادند تا به سهم یوتاکا تانیاما و
گورو شیمورا، یعنی همان دو ریاضیدان ژاپنی که در دهه 1950 بذر کارِ وایلز را
کاشتند، اشاره کنند. گرچه تانیاما بیش از سی سال قبل خودکشی کرده بود، ولی همکار
او شیمورا زنده بود تا شاهد اثبات آن حدس باشد. وقتی از او نظرش را درباره اثبات
پرسیدند، شیمورا به آرامی لبخندی زد و با وقار گفت ”من که قبلاً به شما گفته بودم
درسته!“
مانند
بسیاری از همکاران وایلز، کن ریبت هم احساس میکرد که اثباتِ حدسِ تانیاما-شیمورا
ریاضیات را متحول کرده: ”یک حس روانی قوی در میان ریاضیدانان وجود دارد که میگوید
حالا آنها میتوانند به مسائلی توجه کنند که قبلاً از پرداختن به آنها واهمه داشتند.
حال که شما میدانید کلیه معادلات بیضوی ماجولار هستند، چشمانداز روبرو متفاوت
است، زیرا شما میتوانید قضیهای را برای معادلات بیضوی اثبات کنید و در عین حال
با اینکار به مسئله مشابهای در فرمهای ماجولار حمله کنید، و بالعکس. شما چشمانداز
متفاوتی از اینکه اوضاع از چه قرار است را دارید و کمتر از کار کردن با فرمهای
ماجولار واهمه دارید، زیرا حالا اساساً دارید با معادلات بیضوی کار میکنید. و
البته اگر مقالهای درباره معادلات بیضوی مینویسید، بجای اینکه بگویید ’ما نمیدانیم
که حدس تانیاما-شیمورا درست است یا نه، ولی با فرض اینکه این حدس درست باشد آنگاه
...‘ حالا میگویید ’ما میدانیم که حدس تانیاما-شیمورا درست است، بنابراین فلان،
فلان ... باید درست باشد.‘ این نسبت به قبل حس دلپذیرتری دارد.“
با اثبات
حدس تانیاما-شیمورا وایلز توانسته بود جهانهای ماجولار و بیضوی را با هم متحد
کند، و با اینکار راههای میانبری را برای اثبات مسائل دیگر فراهم آورده بود،
بصورتی که اگر در یکی از این حوزهها مسئلهای حل شد یا قضیهای اثبات شد، این میتوانست
موجب حل مسئله مشابهای در یک حوزه دیگر شود. مسائل حل نشده بیضوی که سابقه آنها
به یونان باستان بازمیگشت حالا میتوانستند با استفاده از کلیه ابزارها وتکنیکهای
ماجولار مورد بازبینی مجدد قرار گیرند.
حتی مهمتر
از این، وایلز اولین قدم در راه طرح متحدسازی لنگلندز (یا همان برنامه لنگلندز)
را برداشته بود. حالا تلاشهای جدیدی درحال انجام بودند که هدف آنها متحدسازی حوزههای
دیگر ریاضیات بود. در ماه مارس 1996 وایلز در جایزه 000,100 دلاری ولف با لنگلندز
سهیم شد (این جایزه را نباید با جایزه ولفسکل اشتباه کنید). کمیته جایزه ولف به
این نتیجه رسید که گرچه اثبات وایلز به تنهایی دست آورد مهمی محسوب میشود، ولی
این اثبات جان تازهای را نیز به طرح جاهطلبانه لنگلندز بخشیده است. در اینجا
پیشرفتی حاصل شده که میتواند ریاضیدانان را به سمت یک دوره طلایی هدایت کند.
بدنبال یک
سال سردرگمی و بلاتکلیفی، حالا جامعه ریاضی میتوانست شادی کند. در هر سمپوزیوم، و
هر کنفرانس ریاضی، حتماً جلسهای بود که به اثبات وایلز اختصاص داشت.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
[1] - شاعر و ادیب یونان باستان (مترجم).
[2] - در ایران این بازی بیشتر در کتابفروشیها
و لوازم تحریر فروشیها بفروش میرسد (مترجم).